C++ - 数値積分(台形則による定積分)!
Updated:
関数 \(f(x)\) の定積分を微小区間に分割して近似値として求める方法を数値積分と言います。
今回は、数値積分の中でも「台形則による定積分」を C++ で挑戦してみました。
まず、\(\displaystyle y=\int_{a} ^ {b}f(x)dx\) を定積分ということは、関数 \(y=f(x)\) の 曲線と x 軸で挟まれた領域の区間 [a, b] の面積を求めるということになります。
そして実際には、以下のように区間 [a, b] を m 個に分割して台形の面積の合計を求めるのです。
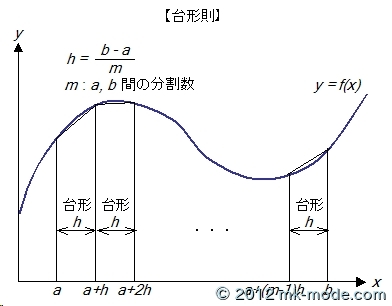
もちろん、分割数を大きくすれば、より正確な値を計算できます。 そして、台形の面積の合計の計算式は以下のようになります。
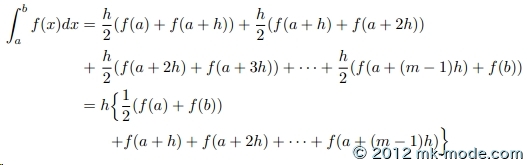
さらに詳しいことは、高校の教科書等で確認してください。
以下、C++ によるサンプルソースです。
0. 前提条件
- Cygwin 1.7.15
- g++ (GCC) 4.7.1
1. C++ ソース作成
今回作成した C++ ソースは以下のとおり。(C++ なのでオブジェクト指向な作りにしている)
被積分関数は \(\sqrt{4-x ^ {2}}\) としている。
区間を [0, 2] とすれば、半径 2 の円の 1/4 の面積(すなわち円周率)が求まる。
File: definite_ingegral_trapezoid.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
/*********************************************
* 台形則による定積分
*********************************************/
#include <iostream> // for cout
#include <math.h> // for sqrt
#include <stdio.h> // for printf()
# define f(x) sqrt(4-x*x) // 被積分関数
using namespace std;
/*
* 計算クラス
*/
class Calc
{
// 各種定数
static const int m = 100; // 積分区間分割数
// 各種変数
double h; // 1区間の幅
double x; // X 値
double s; // 面積
int k; // ループインデックス
public:
// 定積分計算
void calcIntegral(double a, double b);
};
/*
* 定積分計算
*/
void Calc::calcIntegral(double a, double b)
{
// 1区間の幅
h = (b - a) / m;
// 初期化
x = a; // X 値を a で初期化
s = 0; // 面積初期化
// 計算
for (k = 1; k <= m-1; k++) {
x = x + h;
s = s + f(x);
}
s = h * ((f(a) + f(b)) / 2 + s);
// 結果表示
printf(" /%f\n",b);
printf(" | f(x)dx = %f\n", s);
printf(" /%f\n",a);
}
/*
* メイン処理
*/
int main()
{
// 積分区間
double a, b;
try
{
// データ入力
cout << "積分区間 A, B :";
scanf("%lf %lf", &a, &b);
// 計算クラスインスタンス化
Calc objCalc;
// 定積分計算
objCalc.calcIntegral(a, b);
}
catch (...) {
cout << "例外発生!" << endl;
return -1;
}
// 正常終了
return 0;
}
2. C++ ソースコンパイル
$ g++ definite_ingegral_trapezoid.cpp -o definite_ingegral_trapezoid
何も出力されなければ成功。
3. 実行
$ ./definite_ingegral_trapezoid
積分区間 A, B :0 2
/2.000000
| f(x)dx = 3.140417
/0.000000
積分記号(インテグラル)をイメージして出力している。
区間分割数を大きな値にすれば、もっと円周率に近づくでしょう。
このような積分計算をしてみると、コンピュータって本当に「電子計算機」だな、と実感します。
以上。

Comments