C++ - 数値積分(シンプソン則による定積分)!
Updated:
関数 \(f(x)\) の定積分を微小区間に分割して近似値として求める方法を数値積分と言います。
そして、以前「台形則による定積分」についてお話ししました。
今回は、「シンプソン則による定積分」を C++ で実現する方法方法についてです。
まず、台形則では極小区間を直線で近似していたのに対し、シンプソン則では二次曲線で近似します。
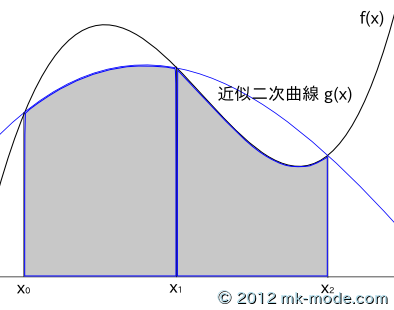
※以下、数式が多いので \(\TeX\) で記載

さらに詳しいことは、高校の教科書等で確認してください。
以下、C++ によるサンプルソースです。
0. 前提条件
- Scientific Linux 6.3 (64bit) での作業を想定。
- g++ (GCC) 4.4.6 20120305 (Red Hat 4.4.6-4)
1. C++ ソース作成
今回作成した C++ ソースは以下のとおり。(C++ なのでオブジェクト指向な作りにしている)
被積分関数は \(\sqrt{4-x ^ {2}}\) としている。
区間を [0, 2] とすれば、半径 2 の円の 1/4 の面積(すなわち円周率)が求まる。
File: definite_ingegral_simpson.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
/*********************************************
* シンプソン則による定積分
*********************************************/
#include <iostream> // for cout
#include <math.h> // for sqrt
#include <stdio.h> // for printf()
# define f(x) sqrt(4-x*x) // 被積分関数
using namespace std;
/*
* 計算クラス
*/
class Calc
{
// 各種定数
static const int m = 100; // 積分区間分割数
// 各種変数
double h; // 1区間の幅
double x; // X 値
double f_o, f_e; // 奇数項の合計、偶数項の合計
double s; // 面積
int k; // ループインデックス
public:
// 定積分計算
void calcIntegral(double a, double b);
};
/*
* 定積分計算
*/
void Calc::calcIntegral(double a, double b)
{
// 1区間の幅
h = (b - a) / (2 * m);
// 初期化
x = a; // X 値を a で初期化
f_o = 0; // 奇数項の合計
f_e = 0; // 偶数項の合計
s = 0; // 面積初期化
// 奇数項の合計、偶数項の合計計算
for (k = 1; k <= 2*m-2; k++) {
x = x + h;
if (k % 2 == 1) {
f_o = f_o + f(x);
} else {
f_e = f_e + f(x);
}
}
// 面積計算
s = f(a) + f(b);
s += 4 * (f_o + f(b-h)) + 2 * f_e;
s *= h / 3;
// 結果表示
printf(" /%f\n",b);
printf(" | f(x)dx = %f\n", s);
printf(" /%f\n",a);
}
/*
* メイン処理
*/
int main()
{
// 積分区間
double a, b;
try
{
// データ入力
cout << "積分区間 A, B :";
scanf("%lf %lf", &a, &b);
// 計算クラスインスタンス化
Calc objCalc;
// 定積分計算
objCalc.calcIntegral(a, b);
}
catch (...) {
cout << "例外発生!" << endl;
return -1;
}
// 正常終了
return 0;
}
2. C++ ソースコンパイル
$ g++ definite_ingegral_simpson -o definite_ingegral_simpson
何も出力されなければ成功。
3. 実行
実際に実行して検証してみる。
$ ./definite_ingegral_simpson
積分区間 A, B :0 2
/2.000000
| f(x)dx = 3.157481
/0.000000
積分記号(インテグラル)をイメージして出力しています。
被積分関数を define で定義しているため、関数値 \(f(x)\) が大きめに丸められており、誤差が若干大きいです。
また、区間分割数を 100 にしていますが、大きな値にすればもっと円周率に近づきます。
さらに、被積分関数によっては台形則より誤差が小さくなったりするので、どちらがよいかは一概には言えません。
以上。

Comments