C++ - 多桁計算！

通常、Ｃ言語等では整数型で扱える数値を超える値の加減乗除はそのままでは計算不可能です。

今回は、データ型を超える整数の加減乗除の方法についてです。

0. 前提条件

• Linux Mint 14 Nadia (64bit) での作業を想定。
• g++ (Ubuntu/Linaro 4.7.2-2ubuntu1) 4.7.2

また、当方の環境で扱える int 型、 long 型の範囲は以下のとおり。

• int : -2,147,483,648 〜 2,147,483,647
• long : -9,223,372,036,854,775,808 〜 9,223,372,036,854,775,807

1. 多桁計算について

加算・減算・乗算・除算ともに数値を指定の桁数で区切って配列として扱って計算する。
配列のサイズは使用環境に合わせて設定するが、当方の環境の場合、 int 型は -2147483648 〜 2147483647 が扱える範囲なので、配列要素１つで８桁扱うようにする。
あとは、筆算をするように計算していけばよい。
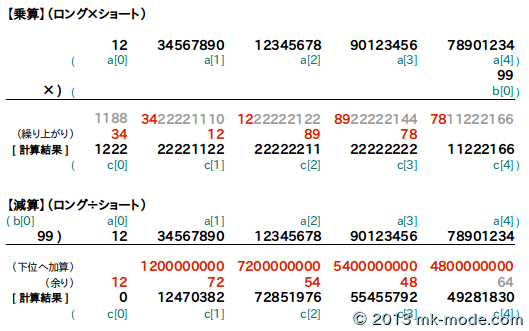
イメージは以下の図のとおり。
また、配列１つで扱える数字を「ショート」、配列２つ以上で扱う数字を「ロング」ということにしている。

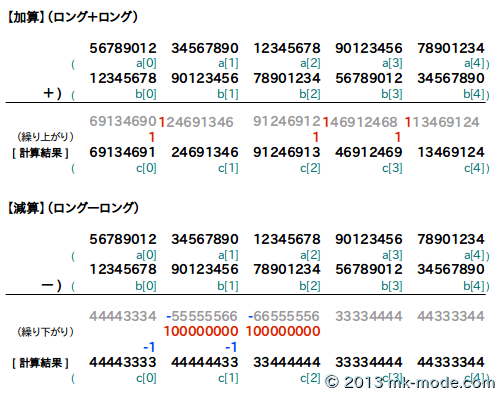
• 加算・・・下位の配列から加算していき、指定の桁数をあふれたらその分を除去し１つ上位に加算していく。
• 減算・・・下位の配列から減算していき、結果が負になったら上位から１借りて加算する。
• 乗算・・・加算同様、下位の配列から乗算していき、指定の桁数をあふれたらその分を除去し１つ上位に加算していく。
• 除算・・・上位の配列から除算していき、余りが発生したらその分を１つ下位へ加算していく。

ちなみに、乗算が何万桁以上になる場合は、この方法ではなく「Karatsuba法」や「Toom-Cook法」や「FFT（高速フーリエ変換）」を使うのが一般的なようだ。

2. C++ ソース作成

例として、以下のようにソースを作成した。

File: calc_big_digits.cpp

/*********************************************
 * 多桁計算
 *********************************************/
#include <iostream>  // for cout
#include <stdio.h>   // for printf()

#define KETA 40  // 最大桁数
#define N    5   // 配列サイズ

using namespace std;

/*
 * 計算クラス
 */
class Calc
{
    // 各種変数
    int i;              // LOOP インデックス
    int carry, borrow;  // 繰り上がり、借り
    long w;             // 被乗数、被除数ワーク
    long remainder;     // 剰余ワーク
    int z[N];           // 計算結果保存用

    public:
        // 計算
        void calc();
        // ロング + ロング
        void ladd(int *, int *);
        // ロング - ロング
        void lsub(int *, int *);
        // ロング * ショート
        void lmul(int *, int);
        // ロング / ショート
        void ldiv(int *, int);
        // 結果出力（ロング用）
        void displayL(int *);
        // 結果出力（ショート用）
        void displayS(int);
};

/*
 * 計算
 */
void Calc::calc()
{
    // 計算する数字（a, b: 加減算用、c, d: 剰除算用、z: 結果格納用）
    int a[N] = {56789012,34567890,12345678,90123456,78901234};
    int b[N] = {12345678,90123456,78901234,56789012,34567890};
    int c[N] = {      12,34567890,12345678,90123456,78901234};
    int d    = 99;

    // ロング + ロング
    ladd(a, b);

    // ロング - ロング
    lsub(a, b);

    // ロング * ショート
    lmul(c, d);

    // ロング / ショート
    ldiv(c, d);
}

/*
 * ロング + ロング
 */
void Calc::ladd(int a[], int b[])
{
    // 計算
    carry = 0;
    for (i = N - 1; i >=0; i--) {
        z[i] = a[i] + b[i] + carry;
        if (z[i] < 100000000) {
            carry = 0;
        } else {
            z[i] = z[i] - 100000000;
            carry = 1;
        }
    }

    // 結果出力
    printf(" ");
    displayL(a);
    printf("+");
    displayL(b);
    printf("=");
    displayL(z);
    printf("\n");
}

/*
 * ロング - ロング
 */
void Calc::lsub(int a[], int b[])
{
    // 計算
    borrow = 0;
    for (i = N - 1; i >=0; i--) {
        z[i] = a[i] - b[i] - borrow;
        if (z[i] >= 0) {
            borrow = 0;
        } else {
            z[i] = z[i] + 100000000;
            borrow = 1;
        }
    }

    // 結果出力
    printf(" ");
    displayL(a);
    printf("-");
    displayL(b);
    printf("=");
    displayL(z);
    printf("\n");
}

/*
 * ロング * ショート
 */
void Calc::lmul(int c[], int d)
{
    // 計算
    carry = 0;
    for (i = N - 1; i >=0; i--) {
        w = c[i];
        z[i] = (w * d + carry) % 100000000;
        carry = (w * d + carry) / 100000000;
    }

    // 結果出力
    printf(" ");
    displayL(c);
    printf("*");
    displayS(d);
    printf("=");
    displayL(z);
    printf("\n");
}

/*
 * ロング / ショート
 */
void Calc::ldiv(int c[], int d)
{
    // 計算
    remainder = 0;
    for (i = 0; i < N; i++) {
        w = c[i];
        z[i] = (w + remainder) / d;
        remainder = ((w + remainder) % d) * 100000000;
    }

    // 結果出力
    printf(" ");
    displayL(c);
    printf("/");
    displayS(d);
    printf("=");
    displayL(z);
    printf("\n");
}

/*
 * 結果出力（ロング用）
 */
void Calc::displayL(int s[])
{
    for (i = 0; i < N; i++)
        printf(" %08d", s[i]);
    printf("\n");
}

/*
 * 結果出力（ショート用）
 */
void Calc::displayS(int s)
{
    for (i = 0; i < N - 1; i++)
        printf(" %8s", " ");
    printf(" %08d\n", s);
}

/*
 * メイン処理
 */
int main()
{
    try
    {
        // 計算クラスインスタンス化
        Calc objCalc;

        // 多桁計算
        objCalc.calc();
    }
    catch (...) {
        cout << "例外発生！" << endl;
        return -1;
    }

    // 正常終了
    return 0;
}

• Gist - C++ source code to compute big-digit values.

3. C++ ソースコンパイル

$ g++ calc_big_digits.cpp -o calc_big_digits

何も出力されなければ成功です。

4. 実行

$ ./calc_big_digits
  56789012 34567890 12345678 90123456 78901234
+ 12345678 90123456 78901234 56789012 34567890
= 69134691 24691346 91246913 46912469 13469124

  56789012 34567890 12345678 90123456 78901234
- 12345678 90123456 78901234 56789012 34567890
= 44443333 44444433 33444444 33334444 44333344

  00000012 34567890 12345678 90123456 78901234
*                                     00000099
= 00001222 22221122 22222211 22222222 11222166

  00000012 34567890 12345678 90123456 78901234
/                                     00000099
= 00000000 12470382 72851976 55455792 49281830

40桁同士の加減算、そして、40桁と小さな数値の乗除算で結果が多桁になる計算ができました。

---

今回は、多桁計算の基本的な考え方でした。
応用して円周率を計算してみたりできますね。

※ちなみに最近の当方の C++ アルゴリズムについての記事は、古い C によるアルゴリズムに関する書物を参考に C++ に移植した形態となっています。

以上。