C++ - 円周率計算（Arctan 系公式）！

今まで、円周率をマチンの公式や Klingensitierna の公式、オイラーの公式で多桁計算する概念、C++ アルゴリズムを紹介しました。

• C++ - 円周率計算（マチンの公式）！
• C++ - 円周率計算（Klingenstierna の公式）！
• C++ - 円周率計算（オイラーの公式）！
• C++ - 円周率計算（オイラーの公式(2)）！

Arctan 系の公式はこれら以外に多数（理論上無数に）ありますが、今回は４つまとめて紹介します。
「Gauß の公式」、「Störmer の公式」２つ、「高野喜久雄の公式」です。

当然、プログラミン言語そのものが保有している三角関数は使用しません。級数展開して計算します。（多桁の円周率計算では、全く無意味ですから。但し、常用対数は影響がないので関数を使用）

また、Arctan 系公式は項数や係数が異るだけなので、１つのプログラムで公式を選択できるようにしています。

0. 前提条件

• Linux Mint 14 Nadia (64bit) での作業を想定。
• g++ (Ubuntu/Linaro 4.7.2-2ubuntu1) 4.7.2
• 多桁計算で使用する1つの配列のサイズは8桁としている。
  （当方の環境で扱える int 型の範囲は -2,147,483,648 〜 2,147,483,647 であることから）
• 指定する桁数は int 型の範囲としているが、あまり大きいと計算に膨大な時間を要するので注意！

1. 公式について

他の Arctan 系の公式と考え方は同じなので、詳細は前述の過去記事を参照のこと。
過去に紹介したものも含めて Arctan 系公式をまとめてみた。

ちなみに、\(\tan ^{-1} = \arctan\) と置き換えてもよい。

2. C++ ソース作成

例として、以下のようにソースを作成した。

• 使用する公式番号を入力するようにしている。
• 計算桁数を入力するようにしている。
• 計算する項数もプログラム内で計算させるようにしている。
• 計算結果をテキストファイルに出力するようにしている。
• ソースは、メイン部分・計算クラス部分・計算クラスプロトタイプ宣言部分の３つに分けるようにした。
• これまでと異るのは、\(x ^ 2\) が8桁を超えるケースが出てくるので、多桁計算ロジックの都合上、\(x\) での除算を2回行うように変更している。（このため、若干処理に時間がかかるようになってしまったが）

File: calc.h

#ifndef INCLUDED_CALC_H
#define INCLUDED_CALC_H

#include <stdio.h>
#include <time.h>

// 出力文字列 ( コンソール、テキストファイル共通 )
#define STR_TITLE   "** Pi Computation by Arctan method **\n"
#define STR_FORMULA "   Formula = [ %s ]\n"
#define STR_DIGITS  "   Digits  = %d\n"
#define STR_TIME    "   Time    = %f seconds\n"
// 多桁計算
#define MAX_DIGITS 100000000  // １つの int で８桁扱う

/*
 * 計算クラス
 */
class Calc
{
    // 各種変数
    int ks;           // 公式・項数
    int kk[12];       // 公式・係数
    int l, l1, n;     // 計算桁数、配列サイズ、計算項数
    int cr, br;       // 多桁計算・繰り上がり、借り
    long w;           // 多桁計算・被乗数、被除数ワーク
    long r;           // 多桁計算・剰余ワーク
    clock_t t1, t2;   // 計算開始CPU時刻、計算終了CPU時刻
    double tt;        // 計算時間
    char *formula;    // 公式名
    char *str_pre;    // 結果出力ファイル名・プリフィックス
    char *str_ext;    // 結果出力ファイル名・拡張子
    char fname[32];   // 結果出力ファイル名
    FILE *out_file;   // 結果出力ファイル名・ポインタ

    public:
        Calc(int, int);                  // コンストラクタ
        void calc();                     // 計算
        void ladd(int *, int *, int *);  // ロング + ロング
        void lsub(int *, int *, int *);  // ロング - ロング
        void lmul(int *, int,   int *);  // ロング * ショート
        void ldiv(int *, int,   int *);  // ロング / ショート
        void display(double, int *);     // 結果出力
};

#endif

File: calc.cpp

#include <math.h>
#include <string.h>
#include "Calc.h"

using namespace std;

/*
 * コンストラクタ
 */
Calc::Calc(int x, int y)
{
    // ==== 各種定数定義
    const char *cst_FORMULA[] = {
        "Machin", "Klingenstierna", "Euler",    "Euler2",
        "Gauss",  "Stormer",        "Stormer2", "Takano"
    };                                              // 公式名
    const char *str_pre = "PI_";                    // 保存ファイル名・プリフィックス
    const char *str_ext = ".txt";                   // 保存ファイル名・拡張子
    const int cst_KS[] = {2, 3, 2, 3, 3, 3, 4, 4};  // 公式の項数
    const int cst_KK[8][12] = {                                 // 公式内係数
        { 16, 1,  5,  -4, 1, 239,   0, 0,   0,  0, 0,      0},  // 1: Machin
        { 32, 1, 10,  -4, 1, 239, -16, 1, 515,  0, 0,      0},  // 2: Klingenstierna
        { 20, 1,  7,   8, 3,  79,   0, 0,   0,  0, 0,      0},  // 3: Euler
        { 16, 1,  5,  -4, 1,  70,   4, 1,  99,  0, 0,      0},  // 4: Euler(2)
        { 48, 1, 18,  32, 1,  57, -20, 1, 239,  0, 0,      0},  // 5: Gauss
        { 24, 1,  8,   8, 1,  57,   4, 1, 239,  0, 0,      0},  // 6: Stormer
        {176, 1, 57,  28, 1, 239, -48, 1, 682, 96, 1,  12943},  // 7: Stormer(2)
        { 48, 1, 49, 128, 1,  57, -20, 1, 239, 48, 1, 110443}   // 8: Takano
    };

    // ==== 各種変数設定
    formula = (char *)cst_FORMULA[x-1];   // 公式名取得
    // 結果出力ファイル名生成
    fname[0] = '\0';
    strcat(fname, str_pre);
    strcat(fname, formula);
    strcat(fname, str_ext);
    printf("\n[ Output file : %s ]\n\n",fname);
    ks = cst_KS[x-1];                     // 計算対象公式の項数
    for (int i = 0; i < ks * 3; i++)
        kk[i] = cst_KK[x-1][i];           // 計算対象公式の係数
    l  = y;                               // 計算桁数
    l1 = (l / 8) + 1;                     // 配列サイズ
    n  = (l / log10(kk[2]) + 1) / 2 + 1;  // 計算項数
}

/*
 * 計算
 */
void Calc::calc()
{
    // ==== 計算開始時刻
    t1 = clock();

    // ==== 配列宣言
    int s[l1 + 2], a[ks][l1 + 2], q[l1 + 2];

    // ==== 配列初期化
    for (int i = 0; i <= l1 + 1; i++) {
        s[i] = q[i] = 0;
        for (int j = 0; j < ks; j++)
            a[j][i] = 0;
    }

    // ==== 計算初期値
    for (int i = 0; i < ks; i++) {
        if (kk[i * 3] >= 0) {
            a[i][0] = kk[i * 3] * kk[i * 3 + 2];
        } else {
            a[i][0] = kk[i * 3] * kk[i * 3 + 2] * -1;
        }
        // 分子が 1 で無ければ、さらに分子の値で除算しておく
        if (kk[i * 3 + 1] != 1)
            ldiv(a[i], kk[i * 3 + 1], a[i]);
    }

    // ==== 計算
    for (int k = 1; k <= n; k++) {
        // 各項の分数計算 ( １つ前の計算結果に追加で除算・乗算 )
        for (int i = 0; i < ks; i++) {
            // 本来 x * x で除算したい（した方が高速だ）が、
            // x が 8桁以下でも x * x が8桁超になるケースがあるため２回に分けている。
            ldiv(a[i], kk[i * 3 + 2], a[i]);
            ldiv(a[i], kk[i * 3 + 2], a[i]);
            if (kk[i * 3 + 1] != 1)  // 分子が 1 でない時
                // 本来 x * x を乗算したい（した方が高速だ）が、
                // x が 8桁以下でも x * x が8桁超になるケースがあるため２回に分けている。
                lmul(a[i], kk[i * 3 + 1], a[i]);
                lmul(a[i], kk[i * 3 + 1], a[i]);
        }

        // 各項の加減算
        for (int i = 1; i < ks; i++) {
            if (kk[i * 3] >= 0) {  // 加算
                if (i == 1)
                    ladd(a[i - 1], a[i], q);
                else
                    ladd(q, a[i], q);
            } else {               // 減算
                if (i == 1)
                    lsub(a[i - 1], a[i], q);
                else
                    lsub(q, a[i], q);
            }
        }

        // 1 / (2 * k - 1) の部分
        ldiv(q, 2 * k - 1, q);

        // 総和計算
        if ((k % 2) != 0)
            ladd(s, q, s);
        else
            lsub(s, q, s);
    }

    // ==== 計算終了時刻
    t2 = clock();

    // ==== 計算時間
    tt = (double)(t2 - t1) / CLOCKS_PER_SEC;

    // ==== 結果出力
    display(tt, s);
}

/*
 * ロング + ロング
 */
void Calc::ladd(int a[], int b[], int c[])
{
    cr = 0;
    for (int i = l1 + 1; i >=0; i--) {
        c[i] = a[i] + b[i] + cr;
        if (c[i] < MAX_DIGITS) {
            cr = 0;
        } else {
            c[i] -= MAX_DIGITS;
            cr = 1;
        }
    }
}

/*
 * ロング - ロング
 */
void Calc::lsub(int a[], int b[], int c[])
{
    br = 0;
    for (int i = l1 + 1; i >=0; i--) {
        c[i] = a[i] - b[i] - br;
        if (c[i] >= 0) {
            br = 0;
        } else {
            c[i] += MAX_DIGITS;
            br = 1;
        }
    }
}

/*
 * ロング * ショート
 */
void Calc::lmul(int d[], int e, int f[])
{
    cr = 0;
    for (int i = l1 + 1; i >=0; i--) {
        w = d[i];
        f[i] = (w * e + cr) % MAX_DIGITS;
        cr = (w * e + cr) / MAX_DIGITS;
    }
}

/*
 * ロング / ショート
 */
void Calc::ldiv(int d[], int e, int f[])
{
    r = 0;
    for (int i = 0; i < l1 + 2; i++) {
        w = d[i];
        f[i] = (w + r) / e;
        r = ((w + r) % e) * MAX_DIGITS;
    }
}

/*
 * 結果出力
 */
void Calc::display(double tt, int s[])
{
    // ==== コンソール出力
    printf(STR_TITLE);
    printf(STR_FORMULA, formula);
    printf(STR_DIGITS, l);
    printf(STR_TIME, tt);

    // ==== ファイル出力
    out_file = fopen(fname, "w");
    fprintf(out_file, STR_TITLE);
    fprintf(out_file, STR_FORMULA, formula);
    fprintf(out_file, STR_DIGITS, l);
    fprintf(out_file, STR_TIME, tt);
    fprintf(out_file, "\n          %d.\n", s[0]);
    for (int i = 1; i < l1; i++) {
        if (i % 10 == 1) fprintf(out_file, "%08d:", (i - 1) * 8 + 1);
        fprintf(out_file, " %08d", s[i]);
        if (i % 10 == 0) fprintf(out_file, "\n");
    }
    fprintf(out_file, "\n\n");
}

File: calc_pi_arctan.cpp

/***********************************************************
 * 円周率計算 by Arctan 系公式
 *
 *    1: Machin
 *    2: Klingenstierna
 *    3: Euler
 *    4: Euler(2)
 *    5: Gauss
 *    6: Stormer
 *    7: Stormer(2)
 *    8: Takano
 *
 * コンパイル方法：
 *   $ g++ Calc.h Calc.cpp CalcPiArctan.cpp -o CalcPiArctan
 **********************************************************/
#include <iostream>
#include "Calc.h"

using namespace std;

/*
 * メイン処理
 */
int main()
{
    int f, n;  // 使用公式番号、計算桁数

    try
    {
        // ==== 使用公式番号入力
        printf("1:Machin, 2:Klingenstierna, 3:Euler, 4:Euler(2),\n");
        printf("5:Gauss, 6:Stormer, 7:Stormer(2), 8:Takano : ");
        scanf("%d", &f);
        if(f < 1 || f > 8) f = 1;  // 範囲外なら 1:Machin と判断

        // ==== 計算桁数入力
        printf("Please input number of Pi Decimal-Digits : ");
        scanf("%d", &n);

        // ==== 計算クラスインスタンス化
        Calc objCalc(f, n);

        // ==== 円周率計算
        objCalc.calc();
    }
    catch (...) {
        // ==== 異常終了
        cout << "例外発生！" << endl;
        return -1;
    }

    // ==== 正常終了
    return 0;
}

• Gist - C++ source code to compute Pi with arctan’s formula.

3. C++ ソースコンパイル

$ g++ calc.h calc.cpp calc_pi_arctan.cpp -o calc_pi_arctan

何も出力されなければ成功です。

4. 実行

実際に実行して検証してみる。
以下では、「高野喜久雄の公式」を使用して小数点以下 10,000 桁を計算している。

$ ./calc_pi_arctan
1:Machin, 2:Klingenstierna, 3:Euler, 4:Euler(2),
5:Gauss, 6:Stormer, 7:Stormer(2), 8:Takano : 8
Please input number of Pi Decimal-Digits : 10000

[ Output file : PI_Takano.txt ]

** Pi Computation by Arctan method **
   Formula = [ Takano ]
   Digits  = 10000
   Time    = 1.180000 seconds

公式別にテキストファイルができているはずである。

File: PI_Takano.txt

** Pi Computation by Arctan method **
   Formula = [ Takano ]
   Digits  = 10000
   Time    = 1.180000 seconds

          3.
00000001: 14159265 35897932 38462643 38327950 28841971 69399375 10582097 49445923 07816406 28620899
00000081: 86280348 25342117 06798214 80865132 82306647 09384460 95505822 31725359 40812848 11174502
00000161: 84102701 93852110 55596446 22948954 93038196 44288109 75665933 44612847 56482337 86783165
00000241: 27120190 91456485 66923460 34861045 43266482 13393607 26024914 12737245 87006606 31558817
00000321: 48815209 20962829 25409171 53643678 92590360 01133053 05488204 66521384 14695194 15116094
00000401: 33057270 36575959 19530921 86117381 93261179 31051185 48074462 37996274 95673518 85752724
00000481: 89122793 81830119 49129833 67336244 06566430 86021394 94639522 47371907 02179860 94370277
00000561: 05392171 76293176 75238467 48184676 69405132 00056812 71452635 60827785 77134275 77896091
00000641: 73637178 72146844 09012249 53430146 54958537 10507922 79689258 92354201 99561121 29021960
00000721: 86403441 81598136 29774771 30996051 87072113 49999998 37297804 99510597 31732816 09631859
00000801: 50244594 55346908 30264252 23082533 44685035 26193118 81710100 03137838 75288658 75332083
00000881: 81420617 17766914 73035982 53490428 75546873 11595628 63882353 78759375 19577818 57780532
00000961: 17122680 66130019 27876611 19590921 64201989 38095257 20106548 58632788 65936153 38182796
        :
===< 途中省略 >===
        :
00009121: 37800297 41207665 14793942 59029896 95946995 56576121 86561967 33786236 25612521 63208628
00009201: 69222103 27488921 86543648 02296780 70576561 51446320 46927906 82120738 83778142 33562823
00009281: 60896320 80682224 68012248 26117718 58963814 09183903 67367222 08883215 13755600 37279839
00009361: 40041529 70028783 07667094 44745601 34556417 25437090 69793961 22571429 89467154 35784687
00009441: 88614445 81231459 35719849 22528471 60504922 12424701 41214780 57345510 50080190 86996033
00009521: 02763478 70810817 54501193 07141223 39086639 38339529 42578690 50764310 06383519 83438934
00009601: 15961318 54347546 49556978 10382930 97164651 43840700 70736041 12373599 84345225 16105070
00009681: 27056235 26601276 48483084 07611830 13052793 20542746 28654036 03674532 86510570 65874882
00009761: 25698157 93678976 69742205 75059683 44086973 50201410 20672358 50200724 52256326 51341055
00009841: 92401902 74216248 43914035 99895353 94590944 07046912 09140938 70012645 60016237 42880210
00009921: 92764579 31065792 29552498 87275846 10126483 69998922 56959688 15920560 01016552 56375678

全ての公式による計算結果が一致することを確認する。

5. 検証

序盤で紹介している8つの公式を使用して、どれがどの程度高速に計算できているのかを検証してみた。
小数点以下 1,000 桁、 10,000 桁、 100,000 桁を５回計算して平均をとってみた。
ちなみに計算に使用したマシンのスペックは以下のとおり。

• CPU: Core2Duo E8500 (3.16GHz)
• メモリ: 3.9 GiB

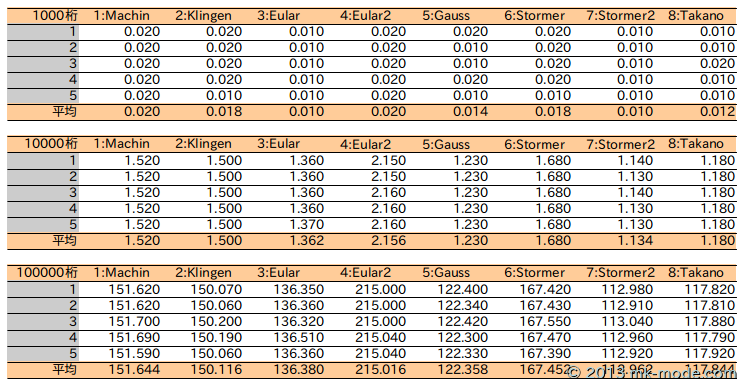
今回の8つの公式の中では、「Störmer の公式(2)」による計算が最も高速で、次が「高野喜久雄の公式」による計算であった。
一般的に発表時期の新しい公式の方が高速であるように感じた。 また、計算する桁数を 10 倍すれば、計算時間は 100 倍になる傾向にある。（そういう計算式だから）

6. 参考サイト

• 円周率を求める公式・アルゴリズム - 円周率.jp -
• πのArctan公式集

---

自分の環境と相談して、計算する桁数を大きくしてみるのもよいでしょう。

ちなみに、結果が何万桁以上になる場合は、多桁（多倍長）乗算に上記の方法ではなく「Karatsuba法」や「Toom-Cook法」や「FFT（高速フーリエ変換）」を使うのが一般的なようです。
これも踏まえて、多桁（多倍長）演算を改良してより高速化に挑んでみたいとも思っている次第です。

以上。