R 言語 - マンデルブロ集合！

統計解析向けのプログラミング言語 R で「マンデルブロ集合」を図形化してみました。

詳しいことは述べません。「こんなこともできるんだ」程度にとどめています。

0. 前提条件

• Linux Mint 14 での作業を想定。
• 統計解析向けのプログラミング言語 R 導入済み。（Ver. 3.0.1 を想定）
• 今回は、２次元グラフと３次元グラフを描画する。

1. マンデルブロ集合について

マンデルブロ集合とは、以下の条件を満たす複素数 \(c\) 全体が作る集合で表される複素平面上の点の集合のことである。

漸化式 \(\begin{eqnarray*} \left\{ \begin{array}{l} z_{n+1}=z_{n}^{2} + c \ (n \in \mathbb{N}) \\ z_{0}=0 \\ \end{array} \right. \end{eqnarray*}\)

で定義される複素数列｛\(z_{n}｜n \in \mathbb{N}\)｝が、 \(n \rightarrow \infty\) で無限大に発散しない。

また、\(z _ {n}\) を点 \((x _ {n}, y _ {n})\) に、\(c\) を点 \((a, b)\) にそれぞれ置き代えて、以下のように変形することもできる。

\[\begin{eqnarray*} \left\{ \begin{array}{l} x_{n+1} = x_{n}^{2} - y_{n}^{2} + a \ (n \in \mathbb{N}) \\ y_{n+1} = 2x_{n}y_{n} + b \ (n \in \mathbb{N}) \end{array} \right. \end{eqnarray*}\]

2. R ライブラリインストール

今回はグラフ描画に ggplot2（２次元）、lattice（３次元）ライブラリを使用するので、未インストールならインストールしておく。

> install.packages("ggplot2")

3. R ソース作成

以下のように R ソースを作成する。

【２次元】

File: mandelbrot_01.R

library(ggplot2)

g <- function(x0, y0) {
  x <- 0
  y <- 0
  for (i in 1:20) {
    xtemp <- x ^ 2 - y ^ 2 + x0
    y <- 2 * x * y + y0
    x <- xtemp
  }
  exp(-(x^2+y^2))
}
m <- 600
X <- seq(-1.8, 0.6, length.out=m)
Y <- seq(-1.2, 1.2, length.out=m)
grid   <- expand.grid(x=X, y=Y)
grid$z <- g(grid$x, grid$y)

ggplot(grid[grid$z != 0, ], aes(x=x, y=y, fill=z)) + geom_tile()

【３次元】

File: mandelbrot_02.R

library(lattice)

g <- function(x0, y0) {
  x <- 0
  y <- 0
  for (i in 1:20) {
    xtemp <- x ^ 2 - y ^ 2 + x0
    y <- 2 * x * y + y0
    x <- xtemp
  }
  exp(-(x^2+y^2))
}
m <- 600
X <- seq(-1.8, 0.6, length.out=m)
Y <- seq(-1.2, 1.2, length.out=m)
grid   <- expand.grid(x=X, y=Y)
grid$z <- g(grid$x, grid$y)

wireframe(z ~ x*y, grid, shade=TRUE)

4. R ソース実行

以下のようにして R ソースを実行してみる。

File: 【２次元】

$ R --vanilla --slave < mandelbrot_01.R

File: 【３次元】

$ R --vanilla --slave < mandelbrot_02.R

5. 確認

R ソースと同じディレクトリに PDF ファイルが作成されるので確認してみる。（ファイル名は２つとも同じなので上書き注意！）

---

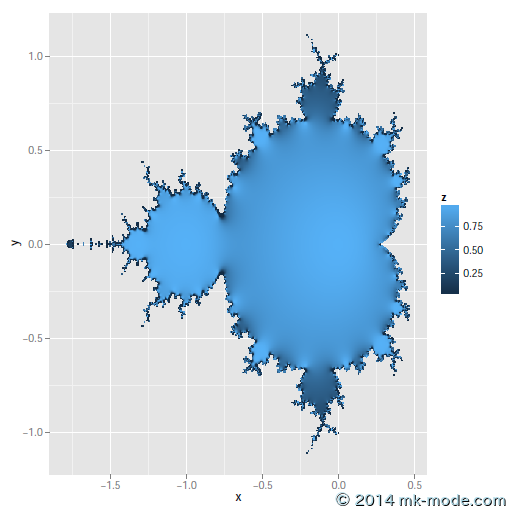
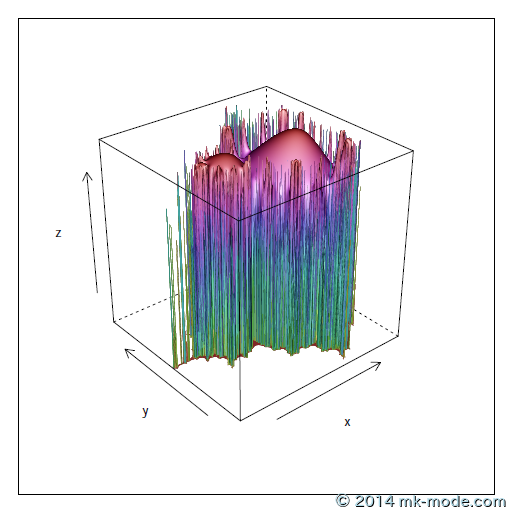
以上。