C++ - 線形計画法(シンプレックス法)!
Updated:
今回は、線形計画法を「シンプレックス法」で解くアルゴリズムを C++ で実装してみました。
以下、簡単な説明と C++ ソースコードの紹介です。
0. 前提条件
- Linux Mint 14 Nadia (64bit) での作業を想定。
- g++ (Ubuntu/Linaro 4.7.2-2ubuntu1) 4.7.2
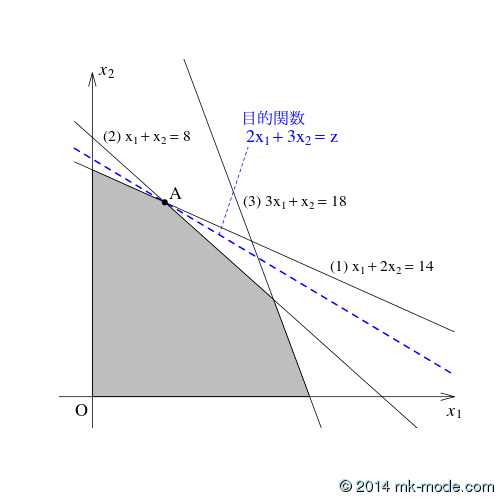
1. 線形計画法(シンプレックス法)について
(数式が多いので、別途 \(\LaTeX\) で作成した文書を貼り付け)




2. C++ ソース作成
以下のように C++ ソールコードを作成してみた。
File: linear_programming.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
/*********************************************
* 線形計画法(シンプレックス法) *
*********************************************/
#include <iostream> // for cout
#include <stdio.h> // for printf()
#define N_ROW 4 // 行数
#define N_COL 6 // 列数
#define N_VAR 2 // 変数の数
using namespace std;
/*
* 計算クラス
*/
class Calc
{
// 各種変数
double min, p, d;
int i, j, k, x, y, flag;
public:
void calcLinearProgramming(); // 線形計画法
};
/*
* 線形計画法
*/
void Calc::calcLinearProgramming()
{
// 係数行列
static double a[N_ROW][N_COL] = {
{ 1.0, 2.0, 1.0, 0.0, 0.0, 14.0},
{ 1.0, 1.0, 0.0, 1.0, 0.0, 8.0},
{ 3.0, 1.0, 0.0, 0.0, 1.0, 18.0},
{-2.0, -3.0, 0.0, 0.0, 0.0, 0.0}
};
while (1) {
// 列選択
min = 9999;
for (k = 0; k < N_COL - 1; k++) {
if (a[N_ROW - 1][k] < min) {
min = a[N_ROW - 1][k];
y = k;
}
}
if (min >= 0) break;
// 行選択
min = 9999;
for (k = 0; k < N_ROW - 1; k++) {
p = a[k][N_COL - 1] / a[k][y];
if (a[k][y] > 0 && p < min) {
min = p;
x = k;
}
}
// ピボット係数
p = a[x][y];
// ピボット係数を p で除算
for (k = 0; k < N_COL; k++)
a[x][k] = a[x][k] / p;
// ピボット列の掃き出し
for (k = 0; k < N_ROW; k++) {
if (k != x) {
d = a[k][y];
for (j = 0; j < N_COL; j++)
a[k][j] = a[k][j] - d * a[x][j];
}
}
}
// 結果出力
for (k = 0; k < N_VAR; k++) {
flag = -1;
for (j = 0; j < N_ROW; j++) {
// ==== 2016-11-14 UPDATE ===>
// if (a[j][k] == 1) flag = j;
if (a[j][k] == 1) {
flag = j;
} else if (flag != -1 && a[j][k] != 0) {
flag = -1;
break;
}
// <=== 2016-11-14 UPDATE ====
}
if (flag != -1)
printf("x%d = %8.4f\n", k, a[flag][N_COL - 1]);
else
printf("x%d = %8.4f\n", k, 0.0);
}
printf("z = %8.4f\n", a[N_ROW - 1][N_COL - 1]);
}
/*
* メイン処理
*/
int main()
{
try
{
// 計算クラスインスタンス化
Calc objCalc;
// 線形計画法
objCalc.calcLinearProgramming();
}
catch (...) {
cout << "例外発生!" << endl;
return -1;
}
// 正常終了
return 0;
}
【2016-11-14 追記)】
※結果出力処理を変更しました。
【追記ここまで】
3. C++ ソースコンパイル
(-Wall は警告出力、-O2 最適化のオプション)
$ g++ -Wall -O2 -o linear_programming linear_programming.cpp
何も出力されなければ成功。
4. 実行
実際に、実行してみる。
$ ./linear_programming
x0 = 2.0000
x1 = 6.0000
z = 22.0000
コンソールには商品の生産量とそのときの売上高が出力される。
「ものづくり」の現場で原価・売上・利益等を考える際に必須となる知識「線形計画法」についてでした。
【2016-11-14 変更】
~※ちなみに、以前 C 言語によるアルゴリズムに関する書物を参考に作成していた C 言語プログラムを C++ に移植した形態となっています。~
※ちなみに、以前 C 言語によるアルゴリズムに関する書物を参考に作成していた C 言語プログラムを C++ に移植した形態となっていますが、そのままでは、特定の条件下での結果出力に不備があるため、結果出力の処理を変更しております。
【変更ここまで】
以上。

Comments