Fortran - 非線形方程式の解法（二分法）！

Fortran 95 で、非線形方程式を二分法を使って解いてみました。

0. 前提条件

• LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
• GCC 6.3.0 (GFortran 6.3.0) でのコンパイルを想定。

1. 二分法による非線形方程式の解法とは？

当ブログ過去記事を参照のこと。

• C++ - 非線形方程式の解法（２分法）！

2. 想定する非線形方程式

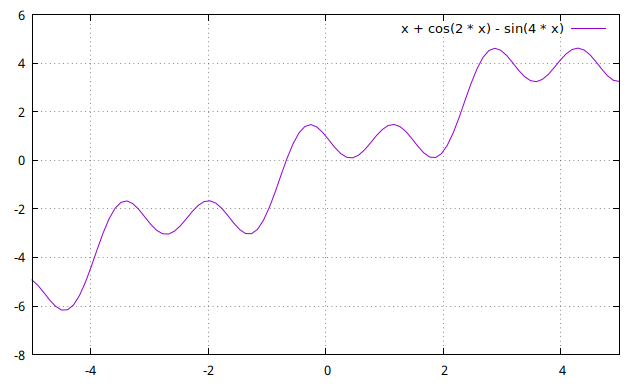
想定する非線形方程式は \(y = x + \cos(2x) - \sin(4x)\)

3. ソースコードの作成

• \(x\)の範囲内に解が1個だけ存在するケースに限定している。

File: nonlinear_equation_bisection.f95

!****************************************************
! 非線形方程式の解法（二分法）
! * 方程式： y = x + cos(2 * x) - sin(4 * x)
!
! date          name            version
! 2018.10.11    mk-mode.com     1.00 新規作成
!
! Copyright(C) 2018 mk-mode.com All Rights Reserved.
!****************************************************
!
program nonlinear_equation_bisection
  implicit none
  ! SP: 単精度(4), DP: 倍精度(8)
  integer,      parameter :: SP = kind(1.0)
  integer(SP),  parameter :: DP = selected_real_kind(2 * precision(1.0_SP))
  integer(SP),  parameter :: NMAX = 50
  real(DP),     parameter :: EPS = 1.0e-6
  logical     :: stat
  integer(SP) :: n
  real(DP)    :: x, y, x_0, x_1, sgn

  write (*, "(a)", advance="no") "x_0, x_1 : "
  read (*,*) x_0, x_1

  ! x_0 > x_1 であれば、交換
  if (x_0 > x_1) then
     x   = x_0
     x_0 = x_1
     x_1 = x
  end if

  ! f(x_0) と f(x_1) の符号が逆なら、終了
  if (f(x_0) * f(x_1) >= 0.0) then
     write (*,*) "f(x_0) * f(x_1) >= 0.0"
     stop
  end if

  sgn = sign(1.0_8, f(x_1) - f(x_0))
  stat = .false.
  do n = 1, NMAX
     x = (x_0 + x_1) * 0.5_8
     y = f(x)

     ! 収束判定
     if (abs(x_1 - x_0) < EPS) then
        stat = .true.
        write(*, '("収束 [", i4, "]")') n
        exit
     else
        write(*, '("誤差 [", i4, "] = ", e20.8)') n, abs(y)
     end if

     ! 次の値を推定
     if (y * sgn < 0.0) then
        x_0 = x
     else
        x_1 = x
     end if
  end do

  ! 結果出力
  if (.not. stat) then
     write (*, *) "近似不可！"
  end if
  write (*, '("近似値 = ", e20.8)') x
  write (*, '("誤差   = ", e20.8)') abs(y)

  stop
contains
  ! 方程式
  ! * f = x + cos(2 * x) - sin(4 * x)
  !
  ! :param  real(8) x
  ! :return real(8) f
  real(DP) function f(x)
    implicit none
    real(DP), intent(in) :: x

    f = x + cos(2 * x) - sin(4 * x)
  end function f
end program nonlinear_equation_bisection

• Gist - Fortran 95 source code to solve nonlinear-equation with bisection method.

4. ソースコードのコンパイル

$ gfortran -o nonlinear_equation_bisection nonlinear_equation_bisection.f95

5. 動作確認

実行すると計算範囲を問われるので、入力する。

$ ./nonlinear_equation_bisection
x_0, x_1 : -5 5
誤差 [   1] =       0.10000000E+01
誤差 [   2] =       0.27603589E+01
誤差 [   3] =       0.30100679E+01
誤差 [   4] =       0.28879451E+00
誤差 [   5] =       0.18085948E+01
誤差 [   6] =       0.75636188E+00
誤差 [   7] =       0.21613569E+00
誤差 [   8] =       0.42745506E-01
誤差 [   9] =       0.85332790E-01
誤差 [  10] =       0.20922182E-01
誤差 [  11] =       0.11008333E-01
誤差 [  12] =       0.49332303E-02
誤差 [  13] =       0.30435341E-02
誤差 [  14] =       0.94335977E-03
誤差 [  15] =       0.10504602E-02
誤差 [  16] =       0.53643335E-04
誤差 [  17] =       0.44483495E-03
誤差 [  18] =       0.19558999E-03
誤差 [  19] =       0.70971872E-04
誤差 [  20] =       0.86639045E-05
誤差 [  21] =       0.22489806E-04
誤差 [  22] =       0.69129736E-05
誤差 [  23] =       0.87545976E-06
誤差 [  24] =       0.30187583E-05
収束 [  25]
近似値 =      -0.67063183E+00
誤差   =       0.10716496E-05

グラフと比較してみると、正しく近似値が求められていることが分かる。

---

以上、