Fortran - 単回帰分析（線形回帰）の決定係数計算！

Fortran 95 で2つの単回帰分析（線形回帰; 単回帰直線）の決定係数を計算してみました。

過去には Ruby で Array クラスを拡張して行なっています。

• Ruby - 単回帰分析（線形回帰）の決定係数計算！

0. 前提条件

• LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
• GCC 6.3.0 (GFortran 6.3.0) でのコンパイルを想定。

1. 決定係数について

当ブログ過去記事を参照のこと。

• Ruby - 単回帰分析（線形回帰）の決定係数計算！

2. ソースコードの作成

• 以下のソースコードでは4種の方法で決定係数を計算している。

File: coefficient_of_determination_line.f95

!****************************************************
! 単回帰分析（線形回帰）決定係数計算
!
!   date          name            version
!   2019.03.31    mk-mode.com     1.00 新規作成
!
! Copyright(C) 2019 mk-mode.com All Rights Reserved.
!****************************************************
!
module const
  ! SP: 単精度(4), DP: 倍精度(8)
  integer,     parameter :: SP = kind(1.0)
  integer(SP), parameter :: DP = selected_real_kind(2 * precision(1.0_SP))
end module const

module comp
  use const
  implicit none
  private
  public :: calc_reg_line, r_2

contains
  ! 単回帰直線計算
  !
  ! :param(in)  real(8) x(:): 説明変数配列
  ! :param(in)  real(8) y(:): 目的変数配列
  ! :param(out) real(8)    a: 切片
  ! :param(out) real(8)    b: 傾き
  ! :param(out) real(8)    r: 相関係数
  subroutine calc_reg_line(x, y, a, b, r)
    implicit none
    real(DP), intent(in)  :: x(:), y(:)
    real(DP), intent(out) :: a, b, r
    integer(SP) :: size_x, size_y, i
    real(DP)    :: sum_x, sum_y, sum_xx, sum_xy
    real(DP)    :: mean_x, mean_y, cov, var_x, var_y

    size_x = size(x)
    size_y = size(y)
    if (size_x == 0 .or. size_y == 0) then
      print *, "[ERROR] array size == 0"
      stop
    end if
    if (size_x /= size_y) then
      print *, "[ERROR] size(X) != size(Y)"
      stop
    end if

    ! 単回帰直線
    sum_x  = sum(x)
    sum_y  = sum(y)
    sum_xx = sum(x * x)
    sum_xy = sum(x * y)
    a = (sum_xx * sum_y - sum_xy * sum_x) &
    & / (size_x * sum_xx - sum_x * sum_x)
    b = (size_x * sum_xy - sum_x * sum_y) &
    & / (size_x * sum_xx - sum_x * sum_x)

    ! 相関係数
    mean_x = sum(x) / size_x
    mean_y = sum(y) / size_x
    cov = sum((x - mean_x) * (y - mean_y))
    var_x = sum((x - mean_x) * (x - mean_x))
    var_y = sum((y - mean_y) * (y - mean_y))
    r = (cov / sqrt(var_x)) / sqrt(var_y)
  end subroutine calc_reg_line

  ! 決定係数 (公式使用)
  !
  ! :param(in)   x: 説明変数配列
  ! :param(in)   y: 目的変数配列
  ! :param(in)   b: 回帰直線の傾き
  ! :return    r_2: 残差の変動
  function r_2(x, y, b)
    implicit none
    real(DP), intent(in) :: x(:), y(:), b
    real(DP) :: r_2
    real(DP) :: sum_x, sum_y, sum_y2, sum_xy
    integer(SP) :: n

    n = size(x)
    sum_x  = sum(x)
    sum_y  = sum(y)
    sum_y2 = sum(y * y)
    sum_xy = sum(x * y)
    r_2 = b * (sum_xy - sum_x * sum_y / n) &
      & / (sum_y2 - sum_y * sum_y / n)
  end function r_2
end module comp

program coefficient_of_determination_line
  use const
  use comp
  implicit none
  character(9), parameter :: F_INP = "input.txt"
  integer(SP),  parameter :: UID   = 10
  real(DP)      :: a, b, r
  real(DP)      :: y_b, s_r, s_y2, s_e
  integer(SP)   :: n, i
  character(20) :: f
  real(DP), allocatable :: x(:), y(:), y_e(:)

  ! IN ファイル OPEN
  open (UID, file = F_INP, status = "old")

  ! データ数読み込み
  read (UID, *) n

  ! 配列メモリ確保
  allocate(x(n))
  allocate(y(n))
  allocate(y_e(n))

  ! データ読み込み
  do i = 1, n
    read (UID, *) x(i), y(i)
  end do
  write (f, '("(A, ", I0, "F8.2, A)")') n
  print f, "説明変数 X = (", x, ")"
  print f, "目的変数 Y = (", y, ")"
  print '(A)', "---"

  ! IN ファイル CLOSE
  close (UID)

  ! 単回帰直線
  call calc_reg_line(x, y, a, b, r)
  print '(A, F12.8)', "    切片 a = ", a
  print '(A, F12.8)', "    傾き b = ", b
  print '(A, F12.8)', "相関係数 r = ", r

  ! 決定係数
  y_e  = a + b * x            ! 推定値
  y_b  = sum(y) / size(y)     ! 標本値 Y （目的変数）の平均
  s_r  = sum((y_e - y_b)**2)  ! 推定値の変動
  s_y2 = sum((y - y_b)**2)    ! 標本値の変動
  s_e  = sum((y - y_e)**2)    ! 残差の変動
  print '(A)', "決定係数"
  ! 解法-1. 決定係数 (= 推定値の変動 / 標本値の変動)
  print '(A, F20.16)', "    R2 (1) = ", s_r / s_y2
  ! 解法-2. 決定係数 (= 1 - 残差の変動 / 標本値の変動)
  print '(A, F20.16)', "    R2 (2) = ", 1.0 - s_e / s_y2
  ! 解法-3. 決定係数 (公式使用(解法-1,2の変形))
  print '(A, F20.16)', "    R2 (3) = ", r_2(x, y, b)
  ! 解法-4. 決定係数 (= 相関係数の2乗)
  print '(A, F20.16)', "    R2 (4) = ", r * r

  ! 配列メモリ解放
  deallocate(x)
  deallocate(y)
  deallocate(y_e)
end program coefficient_of_determination_line

• Gist - Fotran source code to calculate a coefficent of determination for simple linear regression.

3. ソースコードのコンパイル

$ gfortran -o coefficient_of_determination_line coefficient_of_determination_line.f95

4. 動作確認

まず、以下のような入力ファイルを用意する。
（先頭行：点の数、2行目以降：各点）

File: input.txt

10
107  286
336  851
233  589
 82  389
 61  158
378 1037
129  463
313  563
142  372
428 1020

そして、実行。

$ ./coefficient_of_determination_line
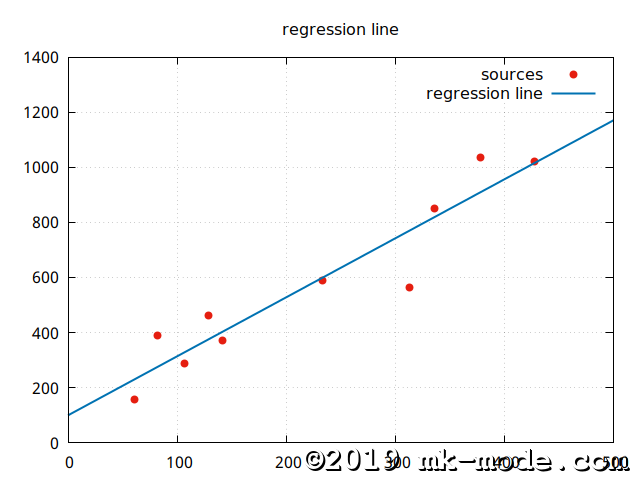
説明変数 X = (  107.00  336.00  233.00   82.00   61.00  378.00  129.00  313.00  142.00  428.00)
目的変数 Y = (  286.00  851.00  589.00  389.00  158.00 1037.00  463.00  563.00  372.00 1020.00)
---
    切片 a =  99.07475877
    傾き b =   2.14452350
相関係数 r =   0.94519501
決定係数
    R2 (1) =   0.8933936043913584
    R2 (2) =   0.8933936043913584
    R2 (3) =   0.8933936043913585
    R2 (4) =   0.8933936043913578

また、参考までに、上記スクリプトで使用した2変量の各点と作成された単回帰直線を gnuplot で描画してみた。

---

以上。