C++ - ローレンツ・アトラクタ(Runge-Kutta 法)
Updated:
C++ でローレンツ・アトラクタの計算をしてみました。
今回は、微分方程式の近似解法に Runge-Kutta(ルンゲ=クッタ)法を使用します。
前回は、微分方程式の近似解法に Euler(オイラー)法を使用しています。
0. 前提条件
- Debian GNU/Linux 10.6 (64bit) での作業を想定。
- GCC 9.2.0 (G++ 9.2.0) (C++17) でのコンパイルを想定。
1. ローレンツ方程式/アトラクタとは
- 「ローレンツ方程式」とは、気象学者「エドワード・N・ローレンツ(Edward N. Lorenz)」が作成した力学系方程式をより単純化した、次のような非線形微分方程式。
パラメータ p, r, b をほんの少し変えるだけで、これらの方程式から得られる軌跡は大きく異なったものになる。
- 「ローレンツ方程式」は、カオス理論を学習する際に序盤で登場する方程式で、カオス研究の先駆的なもの。
- 「アトラクタ」とは、ある力学系がそこに向かって時間発展する集合のことで、カオス理論における研究課題の一つ。
- 「ローレンツ・アトラクタ」とは、ストレンジ・アトラクタの一種。
- 「ローレンツ・アトラクタ」は、言い換えれば、「ローレンツ方程式のカオスのストレンジ・アトラクタ」である。
2. Runge-Kutta(ルンゲ=クッタ)法とは
- Euler 法よりは計算に時間がかかるが、その分、精度も高い。
- 実際の研究等では、 Euler 法ではなく Runge-Kutta 法が使用されることが多い。
- ここでは、 Runge-Kutta 法の詳細については説明しない。
3. C++ ソースコードの作成
- パラメータ p, r, b の値はコマンドライン引数で指定する。
- 計算部分と実行部分とでファイルを分けている。
File: calc.hpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#ifndef LORENZ_ATTRACTOR_EULER_CALC_HPP_
#define LORENZ_ATTRACTOR_EULER_CALC_HPP_
#include <vector>
namespace my_lib {
class Calc {
double p;
double r;
double b;
bool lorenz(const double[], double(&)[3]); // 計算(各ステップ)
public:
Calc(double p, double r, double b) : p(p), r(r), b(b) {} // コンストラクタ
bool lorenz_runge_kutta(std::vector<std::vector<double>>&); // 計算
};
} // namespace my_lib
#endif
File: calc.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include "calc.hpp"
#include <cmath>
#include <iomanip>
#include <iostream>
#include <sstream>
#include <vector>
namespace my_lib {
// 定数
constexpr double kDt = 1.0e-3; // Differential interval
constexpr int kStep = 100000; // Time step count
constexpr double kX0 = 1.0; // Initial value of x
constexpr double kY0 = 1.0; // Initial value of y
constexpr double kZ0 = 1.0; // Initial value of z
/**
* @brief 計算(ローレンツ・アトラクタ(Runge-Kutta 法)
*
* @param[ref] データ配列(計算結果) rec: (vector<vector<double>>)
* @return 真偽(true|false)(bool)
*/
bool Calc::lorenz_runge_kutta(std::vector<std::vector<double>>& res) {
double xyz[] = {kX0, kY0, kZ0};
double xyz_l_0[3]; // 計算用(LorenzAttractor)
double xyz_l_1[3]; // 計算用(LorenzAttractor)
double xyz_l_2[3]; // 計算用(LorenzAttractor)
double xyz_l_3[3]; // 計算用(LorenzAttractor)
double xyz_w[3]; // 計算用(作業用)
unsigned int i; // ループインデックス
unsigned int j; // ループインデックス
try {
for (i = 0; i < kStep; i++) {
if (!lorenz(xyz, xyz_l_0)) return false;
xyz_w[0] = xyz[0] + xyz_l_0[0] * kDt / 2.0;
xyz_w[1] = xyz[1] + xyz_l_0[1] * kDt / 2.0;
xyz_w[2] = xyz[2] + xyz_l_0[2] * kDt / 2.0;
if (!lorenz(xyz_w, xyz_l_1)) return false;
xyz_w[0] = xyz[0] + xyz_l_1[0] * kDt / 2.0;
xyz_w[1] = xyz[1] + xyz_l_1[1] * kDt / 2.0;
xyz_w[2] = xyz[2] + xyz_l_1[2] * kDt / 2.0;
if (!lorenz(xyz_w, xyz_l_2)) return false;
xyz_w[0] = xyz[0] + xyz_l_2[0] * kDt;
xyz_w[1] = xyz[1] + xyz_l_2[1] * kDt;
xyz_w[2] = xyz[2] + xyz_l_2[2] * kDt;
if (!lorenz(xyz_w, xyz_l_3)) return false;
for (j = 0; j < 3; ++j) {
xyz[j] += (xyz_l_0[j] + 2 * xyz_l_1[j] + 2 * xyz_l_2[j] + xyz_l_3[j])
* kDt / 6.0;
}
res.push_back({xyz[0], xyz[1], xyz[2]});
}
} catch (...) {
return false; // 計算失敗
}
return true; // 計算成功
}
bool Calc::lorenz(const double xyz[], double(&xyz_l)[3]) {
try {
xyz_l[0] = -p * xyz[0] + p * xyz[1];
xyz_l[1] = -xyz[0] * xyz[2] + r * xyz[0] - xyz[1];
xyz_l[2] = xyz[0] * xyz[1] - b * xyz[2];
} catch (...) {
return false;
}
return true;
}
} // namespace my_lib
File: lorenz_attractor_runge_kutta.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/***********************************************************
Lorenz attractor (Runge-Kutta method)
DATE AUTHOR VERSION
2020.10.14 mk-mode.com 1.00 新規作成
Copyright(C) 2020 mk-mode.com All Rights Reserved.
***********************************************************/
#include "calc.hpp"
#include <cstdlib> // for EXIT_XXXX
#include <iomanip> // for setprecision
#include <iostream>
#include <string>
#include <vector>
int main(int argc, char* argv[]) {
double p;
double r;
double b;
std::vector<std::vector<double>> res; // データ配列(計算結果)
std::size_t i; // loop インデックス
try {
// コマンドライン引数のチェック
if (argc < 4) {
std::cerr << "[ERROR] Number of arguments is wrong!\n"
<< "[USAGE] ./lorenz_attractor_runge_kutta p r b"
<< std::endl;
return EXIT_FAILURE;
}
// p, r, b の取得
p = std::stod(argv[1]);
r = std::stod(argv[2]);
b = std::stod(argv[3]);
// 計算用オプジェクトのインスタンス化
my_lib::Calc calc(p, r, b);
// 計算
if (!calc.lorenz_runge_kutta(res)) {
std::cout << "[ERROR] Failed to calculare!" << std::endl;
return EXIT_FAILURE;
}
// 結果出力
std::cout << std::fixed << std::setprecision(8);
for (i = 0; i < res.size(); ++i) {
std::cout << std::setw(14) << std::right << res[i][0]
<< std::setw(14) << std::right << res[i][1]
<< std::setw(14) << std::right << res[i][2]
<< std::endl;
}
} catch (...) {
std::cerr << "EXCEPTION!" << std::endl;
return EXIT_FAILURE;
}
return EXIT_SUCCESS;
}
4. ソースコードのコンパイル
まず、以下のように Makefile を作成する。(行頭のインデントはタブ文字)
File: Makefile
gcc_options = -std=c++17 -Wall -O2 --pedantic-errors
lorenz_attractor_euler: lorenz_attractor_runge_kutta.o calc.o
g++ $(gcc_options) -o $@ $^
lorenz_attractor_euler.o : lorenz_attractor_runge_kutta.cpp
g++ $(gcc_options) -c $<
calc.o : calc.cpp
g++ $(gcc_options) -c $<
run : lorenz_attractor_runge_kutta
./lorenz_attractor_runge_kutta
clean :
rm -f ./lorenz_attractor_runge_kutta
rm -f ./*.o
.PHONY : run clean
そして、ビルド(コンパイル&リンク)。
$ make
5. 動作確認
コマンドライン引数に p, r, b の値を指定して実行する。
計算結果が出力される。
$ ./lorenz_attractor_runge_kutta 10 28 2.66666667
:
14.12381298 18.68378846 29.33978919
14.16899368 18.64485725 29.52533963
14.21332423 18.60327057 29.71065962
14.25678662 18.55901971 29.89569240
14.29936294 18.51209735 30.08038071
計算結果をファイルに出力したければ、以下のようにする。
$ ./lorenz_attractor_runge_kutta 10 28 2.66666667 > data.txt
6. 結果確認
参考までに、出力された計算結果を GNUplot で描画してみた。
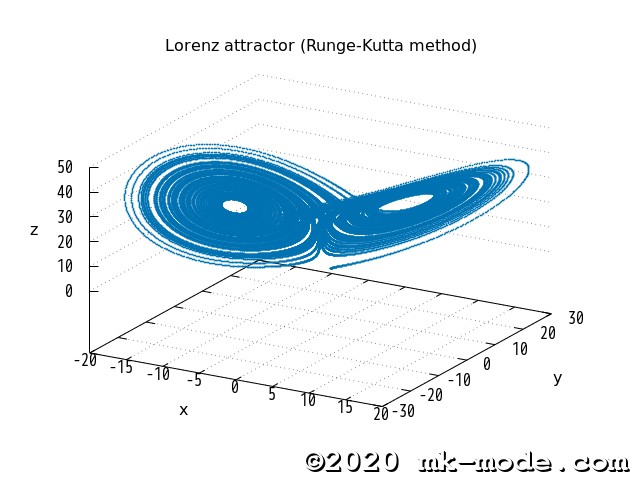
以上。

Comments