Ruby - 多桁乗算（Karatsuba 法）！

前回は、C++ による「多桁乗算（Karatsuba 法）」のアルゴリズムを紹介しました。

• C++ - 多桁乗算（Karatsuba 法）！

今日は、同じアルゴリズムを Ruby で実現してみました。
Ruby では桁数（整数型の範囲）をあまり気にしなくても、メモリの許される限り計算できますが、それでも多桁同士の乗算では不都合になることもあるでしょう。 アルゴリズムについては、上記リンクの過去記事等を参照してください。

実際、ほとんど同じです。

以下、Ruby によるサンプルスクリプトです。

0. 前提条件

• Linux Mint 14 Nadia (64bit) での作業を想定。
• Ruby 2.0.0-p0 を使用。

1. Ruby スクリプト作成

今回作成した Ruby ソースは以下の通り。
スクリプト中の随所にあるテスト用コメントを解除すると、1ループあたりの乗算回数をカウントしたり、100 ループした場合の処理時間を計測するようになっている。
また、近い将来考えていることの準備として、計算可能な最大桁数の設定を 2 のべき乗桁にしている。

File: multiply_karatsuba.rb

#! /usr/local/bin/ruby
#*********************************************
# 多倍長乗算 ( by Karatsuba 法 )
#   - 多倍長 * 多倍長
#   - 最下位の桁を配列の先頭とする考え方
#*********************************************
#
class MultiplyKaratsuba
  D_MAX = 1024 # 計算可能な最大桁数 ( 2のべき乗 )
  D     = 1024 # 実際に計算する桁数 ( D_MAX 以下の 4 の倍数 )

  def initialize
    # ====================================== #
    # テストなので、被乗数・乗数は乱数を使用 #
    # ====================================== #
    @a, @b = Array.new, Array.new
    rnd_a, rnd_b = Random.new(0), Random.new(1)
    # 被乗数・乗数桁数設定
    D.times do |i|
      @a << rnd_a.rand(10)
      @b << rnd_b.rand(10)
    end
  end

  # 計算 ( 標準(筆算)法 )
  def calc_karatsuba
    # 配列初期設定 ( コンストラクタで生成した配列を使用 )
    a, b = @a, @b  # 被乗数配列、乗数配列
    z = Array.new  # 計算結果用配列

    begin
      # 最大桁に満たない部分は 0 を設定
      (D_MAX - a.size).times { |i| a << 0 }
      (D_MAX - b.size).times { |i| b << 0 }
      # ====[ TEST ]===>
      # t1 = Time.now      # 計算開始時刻
      # 100.times do |l|  # 100 回 LOOP
      # @cnt_mul = 0       # 乗算回数リセット
      # <===[ TEST ]====
      # 乗算 ( Karatsuba 法 )
      z = multiply_karatsuba(a, b)
      # ====[ TEST ]===>
      # end
      # t2 = Time.now      # 計算終了時刻
      # @tt = t2 - t1      # 計算時間
      # <===[ TEST ]====
      # 繰り上がり処理
      z = do_carry(z)
      # 結果出力
      display(a, b, z)
    rescue => e
      raise
    end
  end

  private

  # 乗算 ( 標準(筆算)法 )
  def multiply_normal(a, b)
    # 配列サイズ取得
    a_len, b_len = a.size, b.size
    # 計算結果初期化
    z = Array.new(a_len + b_len, 0)
    # 各配列を各桁とみなして乗算
    b_len.times do |j|
      a_len.times do |i|
        z[j + i] += a[i] * b[j]
        # ====[ TEST ]===>
        # @cnt_mul += 1  # 乗算カウント
        # <===[ TEST ]====
      end
    end
    return z
  rescue => e
    raise
  end

  # 乗算 ( Karatsuba 法 )
  def multiply_karatsuba(a, b)
    # 配列サイズ取得
    t_len = a.size
    # ４桁（配列４個）になった場合は標準乗算
    return multiply_normal(a, b)  if t_len <= 4
    # 配列分割
    a_1 = a[(t_len / 2)..-1]
    a_0 = a[0..(t_len / 2 - 1)]
    b_1 = b[(t_len / 2)..-1]
    b_0 = b[0..(t_len / 2 - 1)]
    # v = a1 + a0, w = b1 + b0
    v, w = Array.new, Array.new
    (t_len / 2).times do |i|
      v << a_1[i] + a_0[i]
      w << b_1[i] + b_0[i]
    end
    # x1 = a0 * b0
    x_1 = multiply_karatsuba(a_0, b_0)
    # x2 = a1 * b1
    x_2 = multiply_karatsuba(a_1, b_1)
    # x3 = (a1 + a0) * (b1 + b0)
    x_3 = multiply_karatsuba(v,  w)
    # x3 = x3 - x1 - x2
    t_len.times { |i| x_3[i] -= x_1[i] + x_2[i] }
    # z = x2 * R^2 + (x3 - x2 - x1) * R + x1
    z = x_1 + x_2
    t_len.times { |i| z[i + t_len / 2] += x_3[i] }
    return z
  rescue => e
    raise
  end

  # 繰り上がり処理
  def do_carry(a)
    cr = 0  # 繰り上がり

    begin
      a.size.times do |i|
        a[i] += cr
        cr = a[i] / 10
        a[i] -= cr * 10
      end
      # オーバーフロー時
      puts "[ OVERFLOW!! ] #{cr}" unless cr == 0
      return a
    rescue => e
      raise
    end
  end

  # 結果出力
  def display(a, b, z)
    # 上位桁の不要な 0 を削除するために、配列サイズを取得
    len_a, len_b, len_z = D_MAX, D_MAX, D_MAX * 2
    while a[len_a - 1] == 0 do len_a -= 1 if a[len_a - 1] == 0 end
    while b[len_b - 1] == 0 do len_b -= 1 if b[len_b - 1] == 0 end
    while z[len_z - 1] == 0 do len_z -= 1 if z[len_z - 1] == 0 end
    # a 値
    puts "a ="
    (len_a - 1).downto(0) do |i|
        print a[i]
        print " " if (len_a - i) % 10 == 0
        puts if (len_a - i) % 50 == 0
    end
    puts
    # b 値
    puts "b ="
    (len_b - 1).downto(0) do |i|
        print b[i]
        print " " if (len_b - i) % 10 == 0
        puts if (len_b - i) % 50 == 0
    end
    puts
    # z 値
    puts "z ="
    (len_z - 1).downto(0) do |i|
        print z[i]
        print " " if (len_z - i) % 10 == 0
        puts if (len_z - i) % 50 == 0
    end
    puts; puts
    # ====[ TEST ]====
    # puts "Counts of multiply / 1 loop = #{@cnt_mul}"     # 乗算回数
    # puts "Total time of all loops     = #{@tt} seconds"  # 処理時間
    # ====[ TEST ]====
  rescue => e
    raise
  end
end

if __FILE__ == $0
  begin
    # 計算クラスインスタンス化
    obj = MultiplyKaratsuba.new
    # 乗算 ( Karatsuba 法 )
    obj.calc_karatsuba
  rescue => e
    $stderr.puts "[#{e.class}] #{e.message}"
    e.backtrace.each{ |tr| $stderr.puts "\t#{tr}" }
  end
end

• Gist - Ruby script to multiply big-digit values with Karatsuba method.

2. 実行

まず、実行権限を付与。

$ chmod +x multiply_karatsuba.rb

そして、実行。

$ ./multiply_karatsuba.rb
a =
7993052566 8266064120 9097111427 5774289876 9220210035 
6094933506 4702388611 0101279155 8371352898 5052170975 
3926963548 8731739637 6743795237 0368961910 3122447549 
5194526143 3281479241 8365545146 6582572406 7077163650 
0195786995 7087173085 1831895634 4368860514 5108355450 
7316277206 2677740416 9951088544 9003370047 6315434536 
7000001555 8046599285 1545839232 2526666165 7161294064 
6222369363 0633287892 8428293107 5189445994 2962047204 
7143171320 4503742960 9429732066 1140571121 8714853851 
4523992357 8665157906 5598331564 9556263646 8353285018 
8038209012 2465229172 5695670806 3266793272 1494794231 
9492916303 0723963808 5573950374 6353746871 5593804189 
2365348701 1431212339 6480044413 0541483069 1976637531 
7951496714 4872802947 1638986807 8876699130 0561727532 
5293314745 8058733642 4609407481 7783078833 4840609190 
2995913276 1677525552 4121123739 0448830118 0552048518 
2215779323 7999733543 5793285648 0756363238 8619668298 
8756940813 5690958089 6340348283 8802328883 3606003286 
4192143233 2927209570 2302421050 3951055734 8443446449 
5302763997 1189414865 5400272374 0991073331 8320530349 
8951877618 8674253973 305
b =
7406962534 3269498879 7758624488 0138514732 7547672156 
2285146200 6064210929 2603946403 6444383734 3961641897 
0253894348 4620826253 0429543527 5876496551 9236794638 
6208832937 3820946953 2294258723 4770621711 5139254149 
5020274596 4681816335 2152593700 7073816261 8189614729 
5355229878 1788396494 1205374925 7211236115 9022075013 
2406527382 0691150394 9016440216 8077915939 3526545171 
0748115630 9530042478 6576765791 7567165509 4682888493 
1092820323 7316618099 3689043958 9000885051 0032332621 
5114656411 7997250276 5427167789 0449126034 5265801044 
7721006810 8276362315 6863307639 3214226646 9560360383 
7717767842 0467250503 1633393195 7558856510 6622237413 
5830052400 2342684093 5081578946 9515911702 7088870572 
9264524616 0610374066 8950582250 7983612844 9932804521 
9394300492 4689995926 7460367634 2607402194 9581250627 
7786652594 5976088357 4309307606 9200696966 1371404128 
2071576538 3304423537 6334183092 4803827060 3421530243 
0781185854 5572988644 1939075987 0451215606 4156077266 
2906272132 8910489717 0209477448 7526546803 1177803797 
7208639547 7396897729 4029304184 3915637893 8810196799 
6071977424 2542967100 5985
z =
5920424089 7390532610 0449048020 7708572450 1476445790 
9365457906 5910883189 1331132174 4965328263 9353351322 
7052991161 7322641278 7387898933 2029871191 3960608745 
8559762279 6903824628 2373557557 2978381756 5519737717 
3877862291 6191997852 3264087612 0827484143 7081220122 
7861107782 3917808080 6063312413 4857056174 5146266153 
4279955364 3358317184 8613028798 3721088957 9893156532 
8581959825 2293549941 2197987848 2173489186 2346714538 
8366825393 0197781379 9194605147 8447222353 9183505540 
4029451071 5861384696 5637266583 2032094605 9028532063 
6267446914 2333761740 8432920499 6602754639 3728829690 
9556374047 0787834929 7721750440 5542338514 4973680927 
9455787671 8874626549 2459029172 1631688453 9489095404 
5964277634 8770445317 5231519866 0697559968 1702445406 
9641353090 3025032364 4407208014 1325089338 4164501934 
1172979019 5905034780 6659841527 3858137835 4780538735 
2615874044 7481839536 7073725379 9018054925 1686421460 
8495016498 7792681475 3182738125 0781771741 3341815336 
4625118321 8721477575 5247076764 7637643902 4897996444 
6473500433 7619017662 5133259102 6639792309 2653057206 
2149065710 5580756845 7340480236 9057262428 0375682188 
4221075478 6297812376 0755917527 9276522244 6626325323 
9188445335 2132882454 7554436749 1651557377 5375882773 
1544803975 0017438932 9611639321 3873590885 9238139242 
5384005471 2361798000 1207046515 3263968450 2709672867 
7965176482 6879721635 6373273046 5955334217 4432478933 
1648807917 1524422682 0066018797 1327686809 9391132033 
4724727337 9524643670 9250458898 2763139664 0123548988 
5101157032 9126732981 5290336675 0585775407 1429563057 
5070405323 4673861758 8903590789 9113287776 7853493246 
9711588154 9686641908 7882969904 2263306248 7683938134 
0494265715 4261147471 2054787790 6019886698 6320353270 
0098385009 1723109317 7433930926 8465521602 1619671075 
7021276570 7502918191 7336149373 3941101236 0211981730 
4095670897 3875345966 1124855708 4807212942 3206212176 
8537784809 9992661658 4284692215 3921208115 2987165729 
2759649851 1491250563 0677871704 1395045822 1316264691 
3435716435 4386702886 9850601641 2736343637 5501167273 
4865565979 4396664345 6840367301 3797103744 1990313034 
3003254964 1864102703 7141499881 5261359712 8773968334 
1154253526 2498414253 5029159468 3280434268 5230425

「標準（筆算）法」で計算した結果と一致した。

3. 検証

上記のコードを利用して、乗算回数が何回になるか、計算(100回ループ)にどれくらい時間がかかるかを検証してみた。
乗算回数は予想通り標準（筆算）法より格段に少なくなり、計算にかかる時間も標準（筆算）法より格段に短くなった。
だが、やはり C++ 版による計算より莫大に時間がかかっている。
ちなみに、C++ 版では 1000 回ループの時間を計測したが、Ruby 版では時間がかかりすぎるため 100 回ループの時間を計測した。

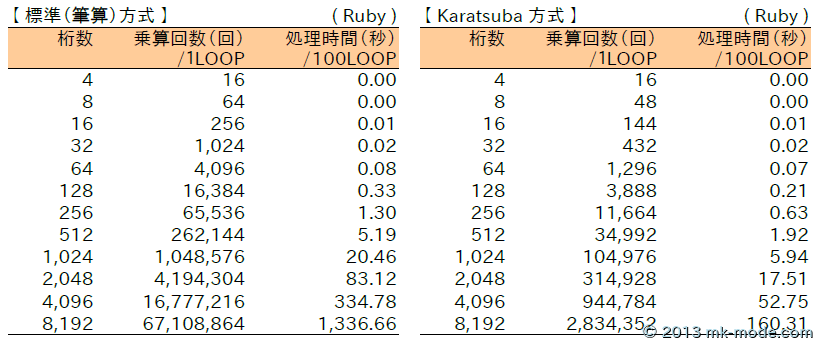
当然ながら、C++ 版の「標準（筆算）法」と「Karatsuba 法」の検証結果グラフと同様なグラフとなった。

---

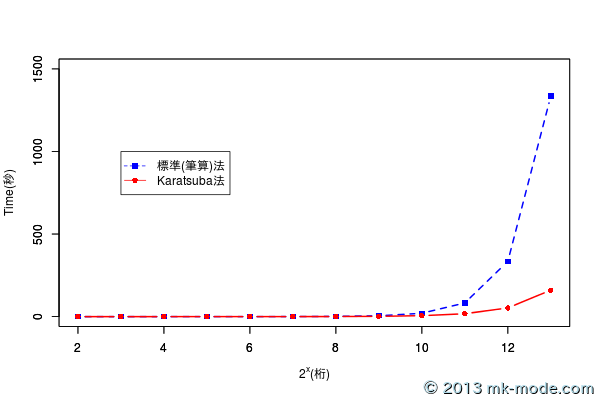
Ruby では “Bignum” クラス内で「Karatsuba 法」を使用している部分もありますが、今回のような方法も理解していおいて無駄ではないでしょう。

以上。