Ruby - フーリエ級数展開!
Updated:
前回は、「フーリエ級数展開」を C++ で実装してみました。
今回は、同じことを Ruby で実装してみました。実際、ほとんど同じです。「フーリエ級数展開」についての詳細は上記の前回記事を参照ください。
0. 前提条件
- Linux Mint 14 Nadia (64bit) での作業を想定。
- Ruby 2.0.0-p0 を使用。
1. Ruby スクリプト作成
File: fourier_series_expansion.rb
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#! /usr/local/bin/ruby
#*********************************************
# フーリエ級数展開
# f(t) = -1 (-pi < t <= 0 )
# 1 ( 0 < t <= pi)
#*********************************************
#
class FourierSeriesExpansion
N = 3 # 計算項数
# フーリエ級数展開
def expand_fourier_series
open("FourierSeriesExpansion.csv", "w") do |f|
# ヘッダ出力
f.puts "t,f(t)"
# 1 / 1000 刻みで計算
y = 0
((Math::PI * -1000).truncate).upto(Math::PI * 1000) do |t|
1.upto(N) { |i| y += calc_term(i, t / 1000.0) }
f.puts "%.3f,%.6f" % [t / 1000.0, 4 / Math::PI * y]
y = 0
end
end
rescue => e
raise
end
private
# 各項計算
def calc_term(n, t)
return Math::sin((2 * n - 1) * t) / (2 * n - 1)
rescue => e
raise
end
end
if __FILE__ == $0
begin
# 計算クラスインスタンス化
obj = FourierSeriesExpansion.new
# フーリエ級数展開
obj.expand_fourier_series
rescue => e
$stderr.puts "[#{e.class}] #{e.message}"
e.backtrace.each{ |tr| $stderr.puts "\t#{tr}" }
end
end
2. 実行
まず、実行権限を付与。
$ chmod +x fourier_series_expansion.rb
そして、実行。
$ ./fourier_series_expansion.rb
コンソールには特に何も表示しない。
アプリと同じディレクトリに FourierSeriesExpansion.csv という CSV ファイルが作成される。
内容は以下のようになっているはず。
File: FourierSeriesExpansion.csv
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
t,f(t)
-3.141,-0.002264
-3.140,-0.006083
-3.139,-0.009903
-3.138,-0.013723
-3.137,-0.017542
-3.136,-0.021361
-3.135,-0.025180
-3.134,-0.028999
-3.133,-0.032817
-3.132,-0.036635
-3.131,-0.040452
-3.130,-0.044269
-3.129,-0.048086
-3.128,-0.051901
-3.127,-0.055717
-3.126,-0.059531
-3.125,-0.063345
-3.124,-0.067159
-3.123,-0.070971
:
====< 途中省略 >====
:
3.122,0.074783
3.123,0.070971
3.124,0.067159
3.125,0.063345
3.126,0.059531
3.127,0.055717
3.128,0.051901
3.129,0.048086
3.130,0.044269
3.131,0.040452
3.132,0.036635
3.133,0.032817
3.134,0.028999
3.135,0.025180
3.136,0.021361
3.137,0.017542
3.138,0.013723
3.139,0.009903
3.140,0.006083
3.141,0.002264
3. グラフ化
数字だけを眺めてもよく分からないので、R でグラフ化(プロット)してみた。
【元の関数グラフ】
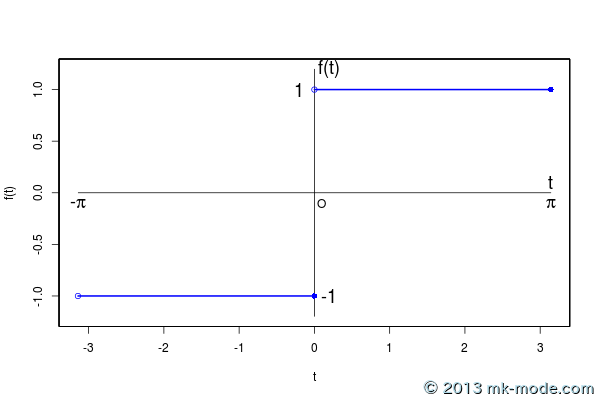
以下、計算項数を 1, 2, 3, 5, 10, 20, 50, 100, 200, 500, 1000, 10000, 100000 個として計算した結果をグラフ化したもの。
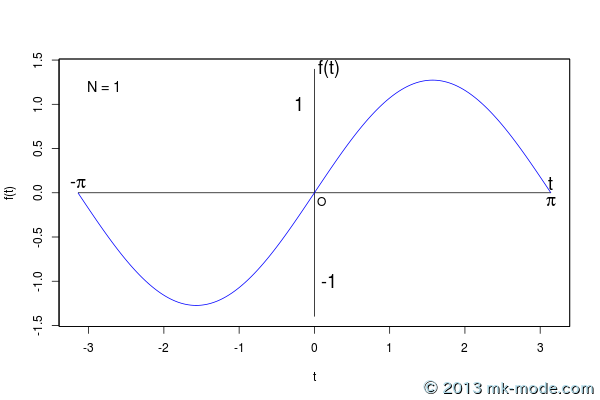
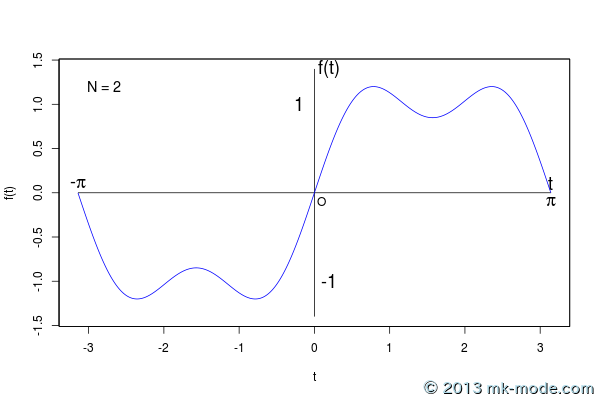
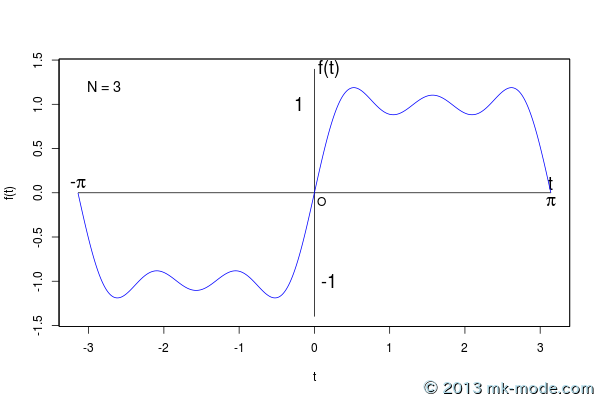
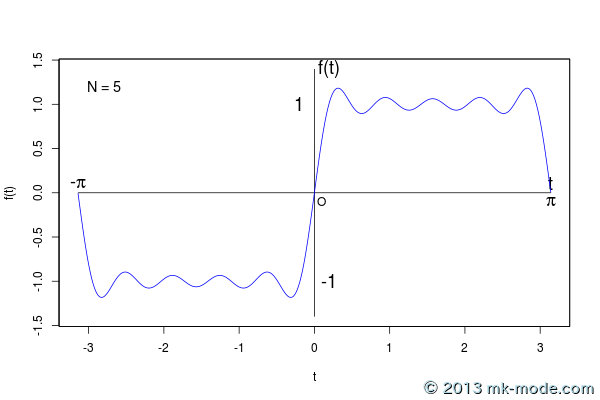
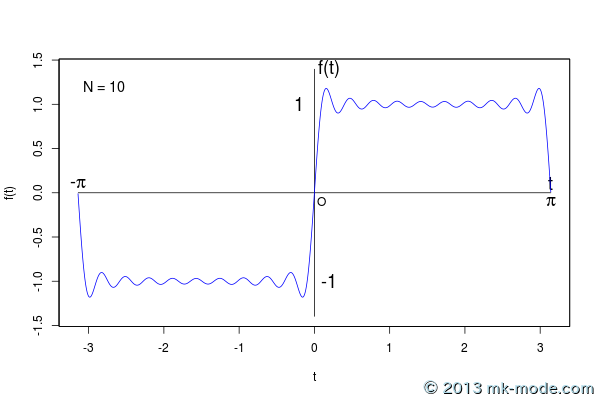
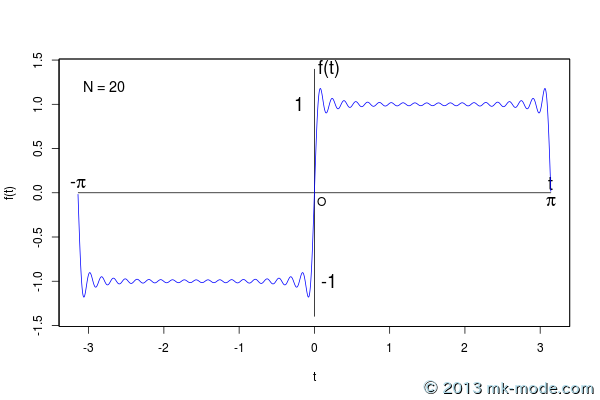
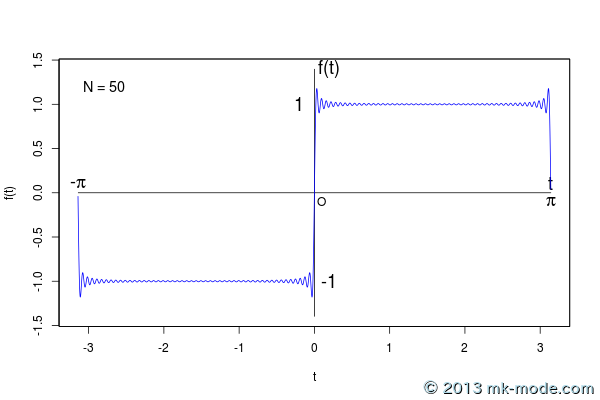
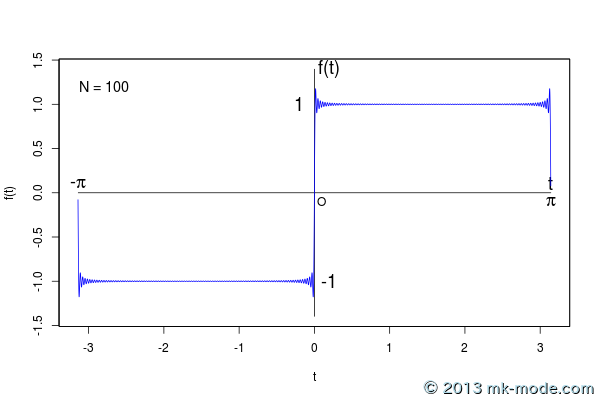
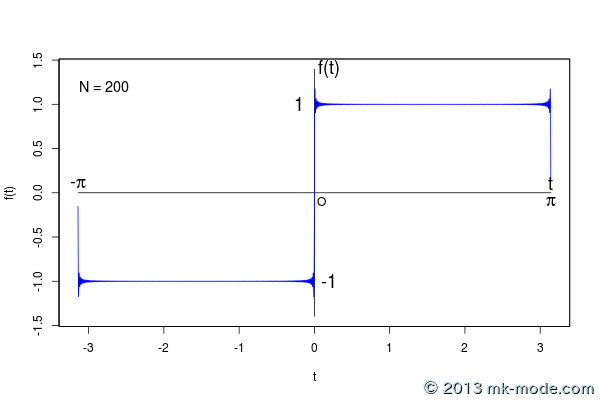
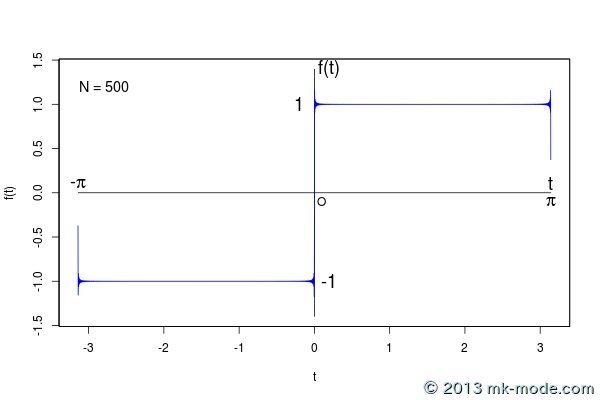
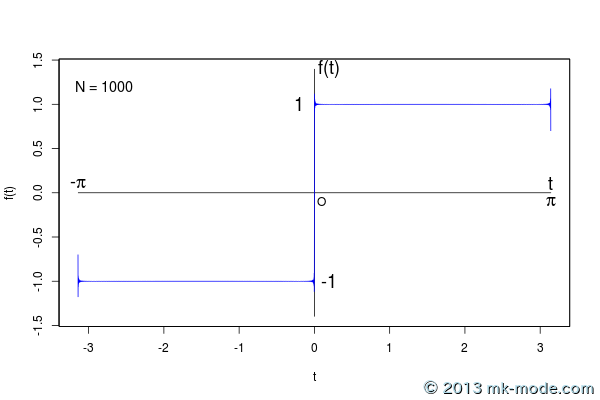
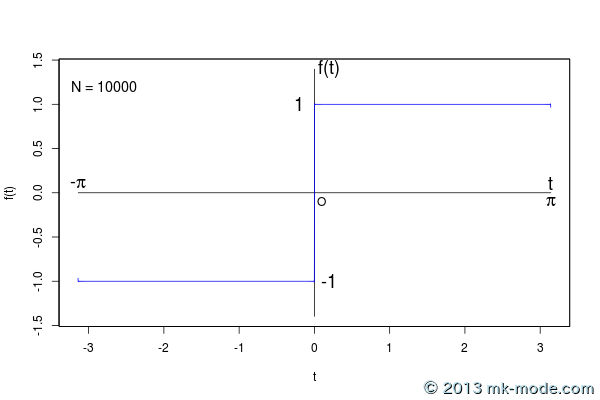
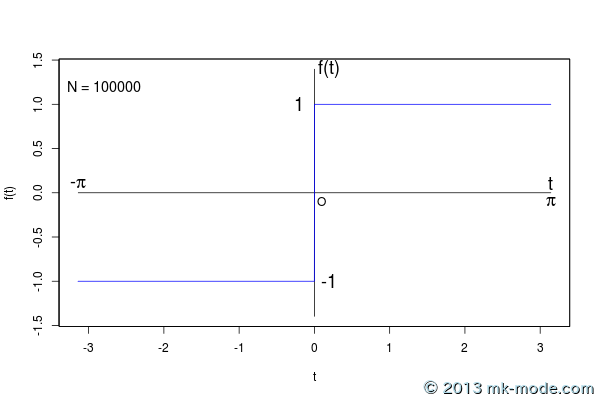
項数を増やすにつれて元の関数のグラフに近付いていくのがよく分かる。
電気工学、音響学、振動、光学等でよく使用する重要な概念です。応用範囲は広いので他にも利用できるかと思います。
以上。

Comments