複素フーリエ級数展開!
Updated:
先日、実形式の「フーリエ級数展開」の C++, Ruby 実装を紹介しました。
今回は、複素形式の「フーリエ級数展開」についてです。
複素数を使用してより簡素な計算式にしようというものであって、展開結果が複素数になるというものではありません。
また、今回は C++ や Ruby への実装はしません。実装しようと思ったら結局「実形式のフーリエ級数展開」になるからです。
以下、「複素フーリエ級数展開」についてです。(数式が多いので、\(\TeX\)で別途作成した文書を切り貼りしている)
1. 概要
今までの「フーリエ級数展開」は「実形式(実フーリエ級数展開)」と呼ばれものであったが、三角関数を使用せず「複素数の指数関数」を使用する形式を「複素形式」の「フーリエ級数展開」または「複素フーリエ級数展開」という。
2. 複素フーリエ級数展開の導出
以下に、「実フーリエ級数展開」の定義から「複素フーリエ級数展開」を導出する手順について記述する。


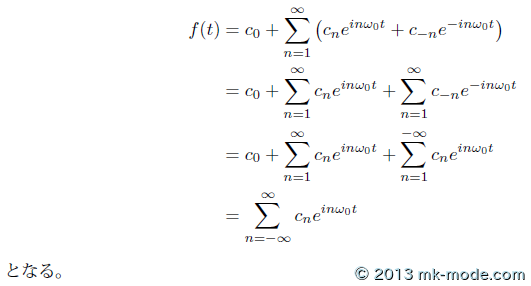

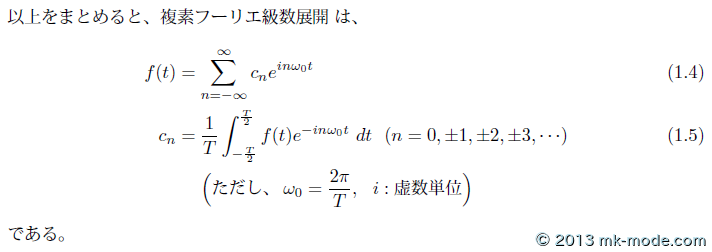
上記の (1.1), (1.2), (1.3) が「(実)フーリエ級数展開」の定義、(1.4), (1.5) が「複素フーリエ級数展開」の定義である。
3. 例題
例題として、実際に周期関数を複素フーリエ級数展開してみる。
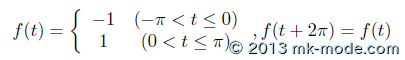
t の範囲は -\(\pi \sim \pi\) に限定している。
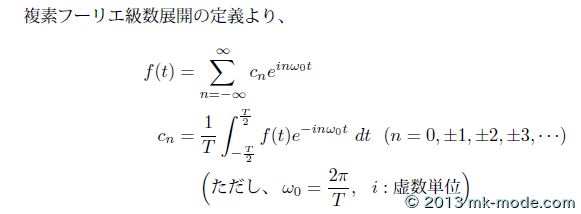
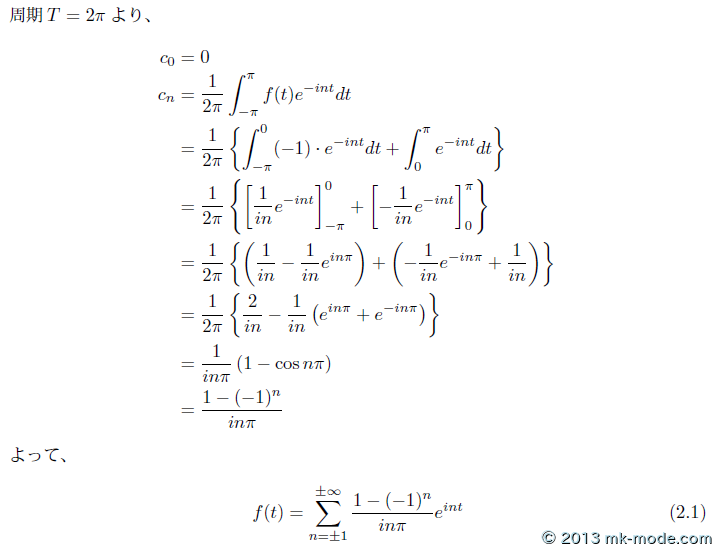
前回の実フーリエ級数展開とは異なる(三角関数を使用せず、複素数の指数関数を使用した)結果となった。
4. 実形式と複素形式のフーリエ級数展開の整合性確認
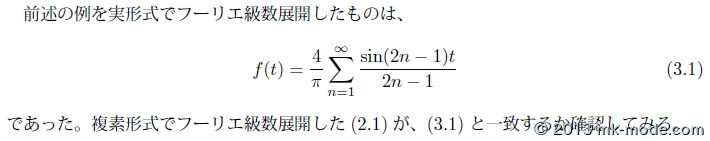

「(実)フーリエ級数展開」、「複素フーリエ級数展開」とも、電気工学、音響学、振動、光学等でよく使用する重要な概念です。応用範囲は広いので他にも利用できるかと思います。
以上。

Comments