Ruby - Array クラス拡張で単回帰直線計算！

２変量の「単回帰直線」の「切片」と「傾き」を Ruby で簡単に計算するように試してみました。

Array クラスを拡張する方法です。

それほど難しい数学的アルゴリズムでも、それほど難しいプログラミングロジックでもありませんが、少し頻繁に使用することになりそうなので試してみた次第です。

0. 前提条件

• Ruby 2.1.3-p242 での作業を想定。

1. 単回帰直線について

まず、簡単に単回帰直線について。
（数式が多いので、別途 \(\LaTeX\) で作成した文書を貼り付け）

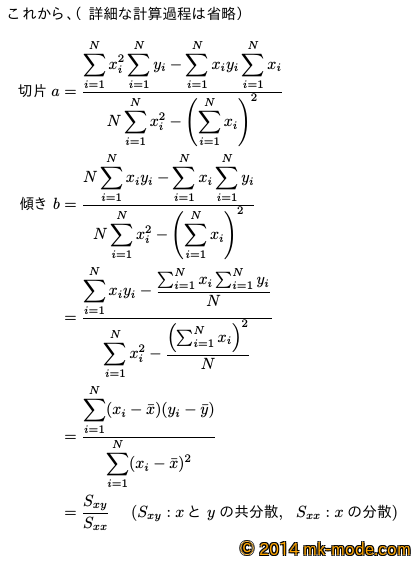
説明変数\(x\)が1次だったので「単回帰『直線』」と呼んでいたが、2次以上なら「単回帰『曲線』」と呼ぶことになる。
また、説明変数が2種類以上ある場合は「重回帰曲線」と呼ぶ。

さらに、回帰直線・曲線を求めたり、これらを使用して分析したりすることを「回帰分析」と呼ぶ。

2. Ruby スクリプト作成

以下のように Array クラスを拡張してメソッドを定義してみた。

File: regression_line.rb

class Array
  def reg_line(y)
    # 以下の場合は例外スロー
    # - 引数の配列が Array クラスでない
    # - 自身配列が空
    # - 配列サイズが異なれば例外
    raise "Argument is not a Array class!"  unless y.class == Array
    raise "Self array is nil!"              if self.size == 0
    raise "Argument array size is invalid!" unless self.size == y.size

    # x の総和
    sum_x = self.inject(0) { |s, a| s += a }
    # y の総和
    sum_y = y.inject(0) { |s, a| s += a }
    # x^2 の総和
    sum_xx = self.inject(0) { |s, a| s += a * a }
    # x * y の総和
    sum_xy = self.zip(y).inject(0) { |s, a| s += a[0] * a[1] }
    # 切片 a
    a  = sum_xx * sum_y - sum_xy * sum_x
    a /= (self.size * sum_xx - sum_x * sum_x).to_f
    # 傾き b
    b  = self.size * sum_xy - sum_x * sum_y
    b /= (self.size * sum_xx - sum_x * sum_x).to_f
    {intercept: a, slope: b}
  end
end

# 説明変数と目的変数
ary_x = [107, 336, 233, 82, 61, 378, 129, 313, 142, 428]
ary_y = [286, 851, 589, 389, 158, 1037, 463, 563, 372, 1020]
puts "説明変数 X = {#{ary_x.join(', ')}}"
puts "目的変数 Y = {#{ary_y.join(', ')}}"
puts "---"

# 単回帰直線算出（切片と傾き）
reg_line = ary_x.reg_line(ary_y)
puts "切片 a = #{reg_line[:intercept]}"
puts "傾き b = #{reg_line[:slope]}"

• Gist - Ruby script to calculate a simple lenear regression line.

3. Ruby スクリプト実行

実行してみる。

$ ruby regression_line.rb
説明変数 X = {107, 336, 233, 82, 61, 378, 129, 313, 142, 428}
目的変数 Y = {286, 851, 589, 389, 158, 1037, 463, 563, 372, 1020}
---
切片 a = 99.07475877245791
傾き b = 2.144523500351028

4. 視覚的な確認

参考までに、上記スクリプトで使用した2変量の各点と作成された単回帰直線を R でグラフに描画してみた。

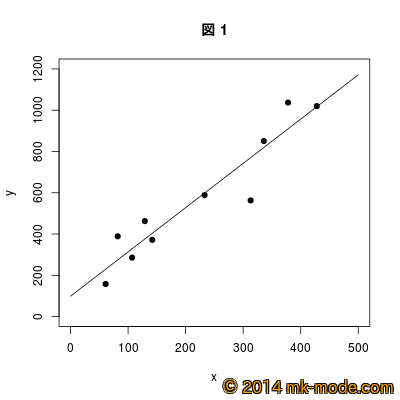
当然ながら、よくあるそれらしいグラフとなった。

---

このメソッドを応用して、相関のある２変量での予測が可能となります。

以上。