Python - ローレンツ・アトラクタ(Runge-Kutta 法)!
Updated:
先日、 Ruby でローレンツ・アトラクタを計算&描画しました。
そして、前回、 Python で微分方程式の近似解法に Euler(オイラー)法を使用して、ローレンツ・アトラクタを計算&描画しました。
今回は、微分方程式の近似解法に Runge-Kutta(ルンゲ=クッタ)法を使用して、計算&描画してみました。(Python で)
0. 前提条件
- Python 3.6.4 (エンコード:UTF-8)での作業を想定。
1. ローレンツ方程式/アトラクタとは
- 「ローレンツ方程式」とは、気象学者「エドワード・N・ローレンツ(Edward N. Lorenz)」が作成した力学系方程式をより単純化した、次のような非線形微分方程式。
パラメータ p, r, b をほんの少し変えるだけで、これらの方程式から得られる軌跡は大きく異なったものになる。
- 「ローレンツ方程式」は、カオス理論を学習する際に序盤で登場する方程式で、カオス研究の先駆的なもの。
- 「アトラクタ」とは、ある力学系がそこに向かって時間発展する集合のことで、カオス理論における研究課題の一つ。
- 「ローレンツ・アトラクタ」とは、ストレンジ・アトラクタの一種。
- 「ローレンツ・アトラクタ」は、言い換えれば、「ローレンツ方程式のカオスのストレンジ・アトラクタ」である。
2. Runge-Kutta(ルンゲ=クッタ)法とは
- Euler 法よりは計算に時間がかかるが、その分、精度も高い。
- 実際の研究等では、 Euler 法ではなく Runge-Kutta 法が使用されることが多い。
- ここでは、 Runge-Kutta 法の詳細については説明しない。
3. Python スクリプトの作成
- 数値演算ライブラリ NumPy は使用しない。(使用するほどでもないので)
- グラフ描画には “matplotlib” ライブラリを使用。(要インストール)
- パラメータ
p,r,bのデフォルト値は10,28,8/3としている。
変更したければ、lorenzメソッド呼び出し時に引数で指定する。 - 今回使用するのは4次の Runge-Kutta 法。
- 実際、ローレンツ・アトラクタを計算する際に計算の粗い Euler 法を使用することはあまりなく、 Runge-Kutta 法で計算することが多い。
File: lorenz_attractor_runge_kutta.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#! /usr/local/bin/python3.6
"""
Lorenz attractor (Runge-Kutta method)
"""
import sys
import traceback
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
class LorenzAttractorRungeKutta:
DT = 1e-3 # Differential interval
STEP = 100000 # Time step count
X_0, Y_0, Z_0 = 1, 1, 1 # Initial values of x, y, z
def __init__(self):
self.res = [[], [], []]
def exec(self):
""" Loranz attractor (Runge-Kutta method) execution """
try:
xyz = [self.X_0, self.Y_0, self.Z_0]
for _ in range(self.STEP):
k_0 = self.__lorenz(xyz)
k_1 = self.__lorenz([
x + k * self.DT / 2 for x, k in zip(xyz, k_0)
])
k_2 = self.__lorenz([
x + k * self.DT / 2 for x, k in zip(xyz, k_1)
])
k_3 = self.__lorenz([
x + k * self.DT for x, k in zip(xyz, k_2)
])
for i in range(3):
xyz[i] += (k_0[i] + 2 * k_1[i] + 2 * k_2[i] + k_3[i]) \
* self.DT / 6.0
self.res[i].append(xyz[i])
self.__plot()
except Exception as e:
raise
def __lorenz(self, xyz, p=10, r=28, b=8/3.0):
""" Lorenz equation
:param list xyz
:param float p
:param float r
:param float b
:return list xyz
"""
try:
return [
-p * xyz[0] + p * xyz[1],
-xyz[0] * xyz[2] + r * xyz[0] - xyz[1],
xyz[0] * xyz[1] - b * xyz[2]
]
except Exception as e:
raise
def __plot(self):
""" Protting """
try:
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
ax.set_title("Lorenz attractor (Runge-Kutta method)")
ax.plot(self.res[0], self.res[1], self.res[2], color="red", lw=1)
#plt.show()
plt.savefig("lorenz_attractor_runge_kutta.png")
except Exception as e:
raise
if __name__ == '__main__':
try:
obj = LorenzAttractorRungeKutta()
obj.exec()
except Exception as e:
traceback.print_exc()
sys.exit(1)
4. Ruby スクリプトの実行
まず、実行権限を付与。
$ chmod +x lorenz_attractor_runge_kutta.py
そして、実行。
$ ./lorenz_attractor_runge_kutta.py
5. 結果確認
Python スクリプトと同じディレクトリ内に “lorenz_attractor_runge_kutta.png” という画像ファイルが作成されるので、確認してみる。
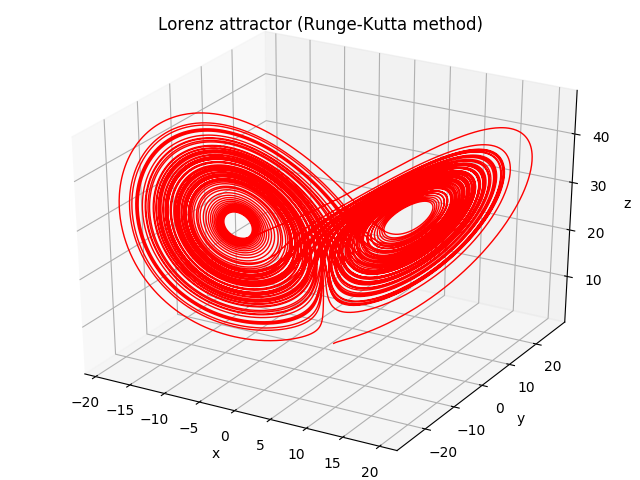
以上。

Comments