Fortran - フーリエ級数展開!
Updated:
Fortran 95 でフーリエ級数展開を実装する方法についての記録です。
0. 前提条件
- LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
- GCC 6.3.0 (GFortran 6.3.0) でのコンパイルを想定。
1. アルゴリズムについて
当ブログ過去記事を参照のこと。
2. ソースコードの作成
- 計算項数の取得は標準入力から。(コマンドライン引数ではない)
File: fourier_series_expansion.f95
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
!****************************************************
! フーリエ級数展開
! f(t) = -1 (-PI < t <= 0 )
! 1 ( 0 < t <= PI)
!
! date name version
! 2018.12.14 mk-mode.com 1.00 新規作成
!
! Copyright(C) 2018 mk-mode.com All Rights Reserved.
!****************************************************
!
module const
! SP: 単精度(4), DP: 倍精度(8)
integer, parameter :: SP = kind(1.0)
integer(SP), parameter :: DP = selected_real_kind(2 * precision(1.0_SP))
real(DP), parameter :: PI = 4.0_DP * atan(1.0_DP)
end module const
module fourier
use const
implicit none
private
public :: expand
contains
! フーリエ級数展開
! * 結果出力も行う
!
! :param(in) integer(4) n: 計算項数
subroutine expand(n)
implicit none
integer(SP), intent(in) :: n
integer(SP) :: t, i
real(DP) :: y
y = 0.0_DP
do t = int(-1000.0_DP * PI), int(1000.0_DP * PI)
do i = 1, n
y = y + calc_term(i, t / 1.0e3_DP)
end do
print '(F6.3, X, F9.6)', t / 1.0e3_DP, 4.0_DP / PI * y
y = 0.0_DP
end do
end subroutine expand
! 各項計算
function calc_term(n, t) result(c)
implicit none
integer(SP), intent(in) :: n
real(DP), intent(in) :: t
real(DP) :: c
c = sin((2 * n - 1) * t) / (2 * n - 1)
end function calc_term
end module fourier
program fourier_series_expansion
use const
use fourier
implicit none
integer(SP) :: n, t
! 計算項数の取得
read (*, *) n
! フーリエ級数展開
call expand(n)
end program fourier_series_expansion
3. ソースコードのコンパイル
$ gfortran -o fourier_series_expansion fourier_series_expansion.f95
4. 動作確認
計算項数を 1, 2, 3, 5, 10, 20, 50, 100, 200, 500, 1000, 10000, 100000 と変化させて実行し、それぞれテキストファイルに出力する。
$ echo 1 | ./fourier_series_expansion > n_1.txt
$ echo 2 | ./fourier_series_expansion > n_2.txt
$ echo 3 | ./fourier_series_expansion > n_3.txt
$ echo 5 | ./fourier_series_expansion > n_5.txt
$ echo 10 | ./fourier_series_expansion > n_10.txt
$ echo 20 | ./fourier_series_expansion > n_20.txt
$ echo 50 | ./fourier_series_expansion > n_50.txt
$ echo 100 | ./fourier_series_expansion > n_100.txt
$ echo 200 | ./fourier_series_expansion > n_200.txt
$ echo 500 | ./fourier_series_expansion > n_500.txt
$ echo 1000 | ./fourier_series_expansion > n_1000.txt
$ echo 10000 | ./fourier_series_expansion > n_10000.txt
$ echo 100000 | ./fourier_series_expansion > n_100000.txt
5. 結果確認
GNUPLOT で描画してみた。
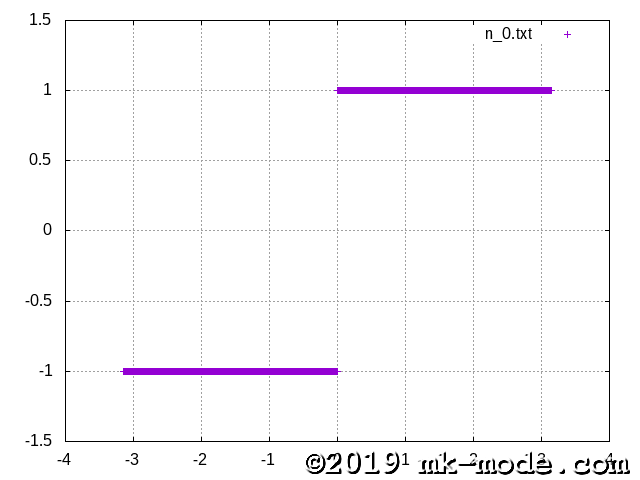
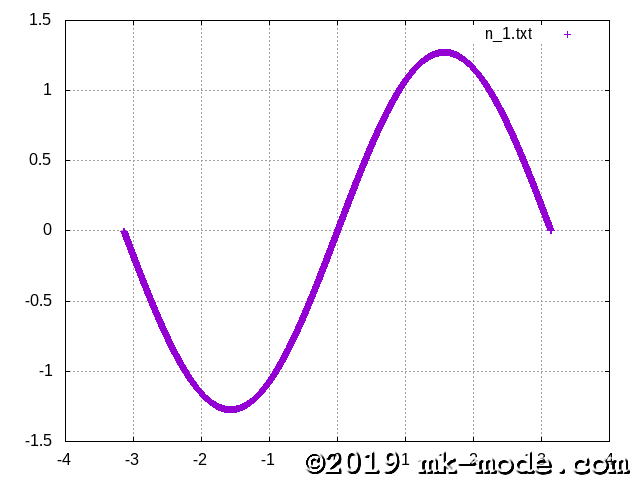
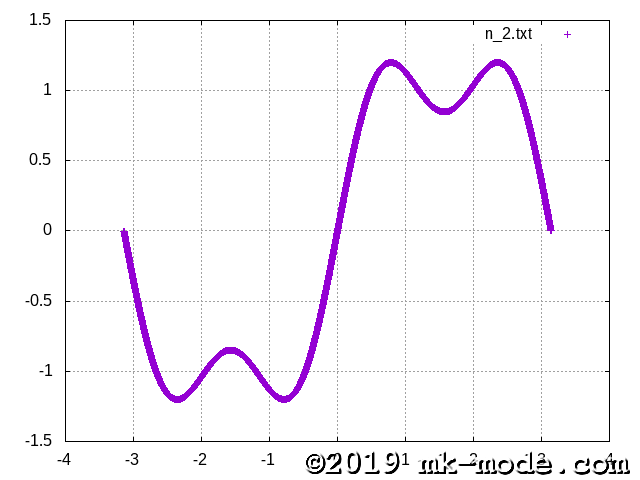
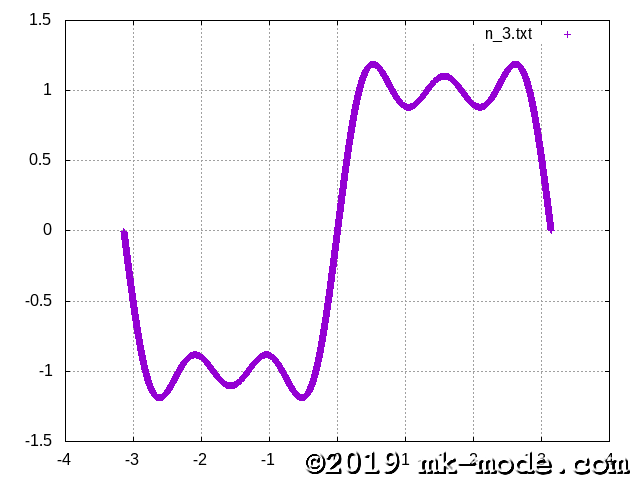
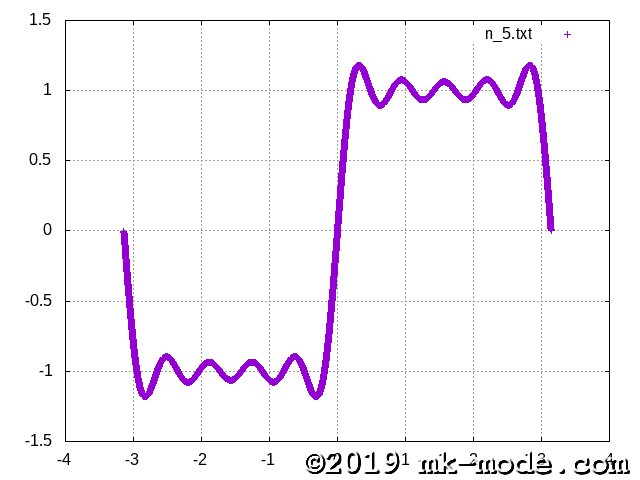
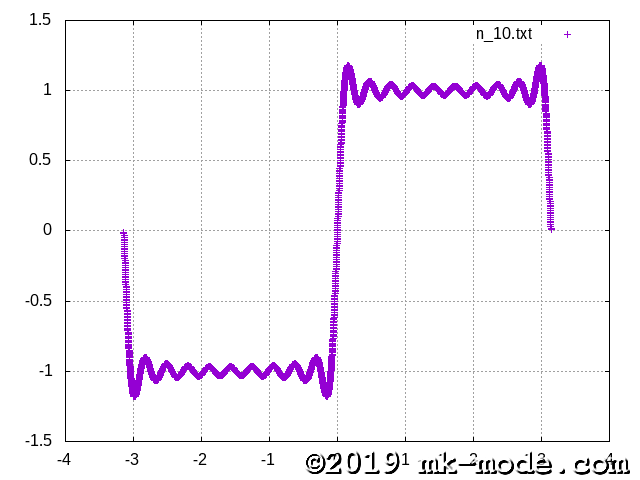
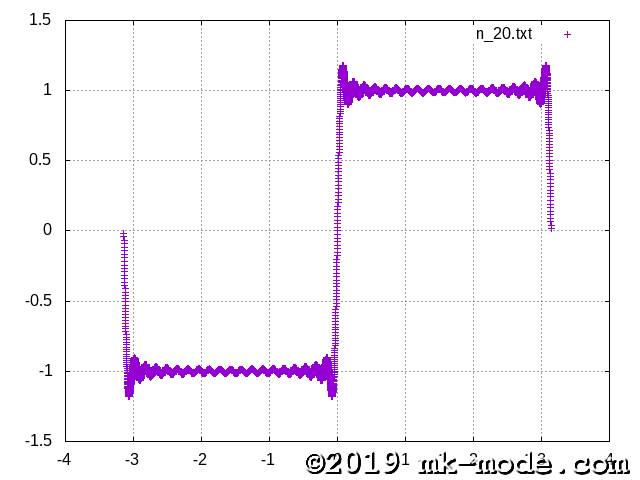
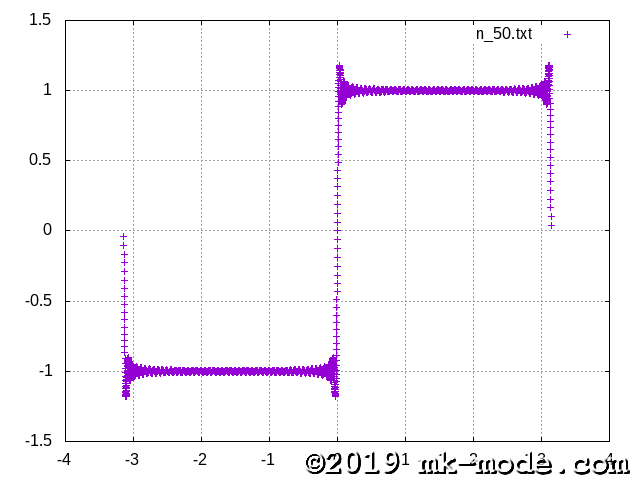
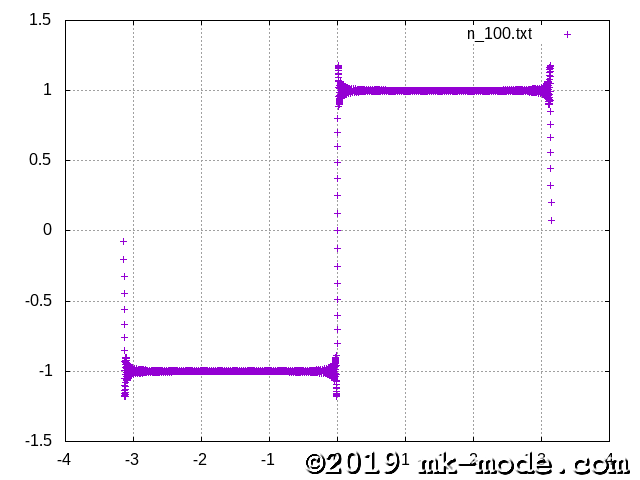
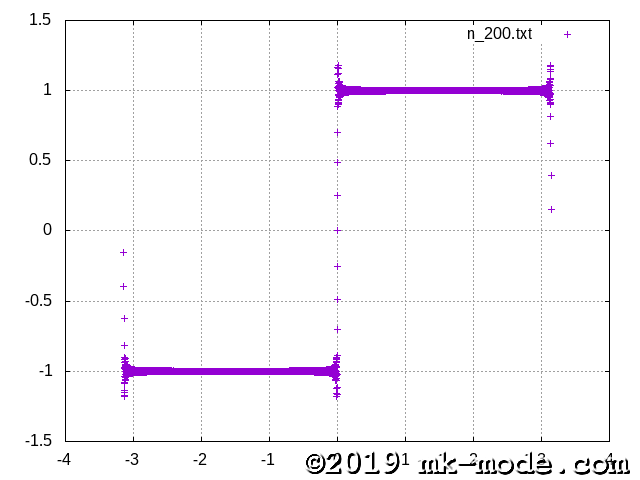
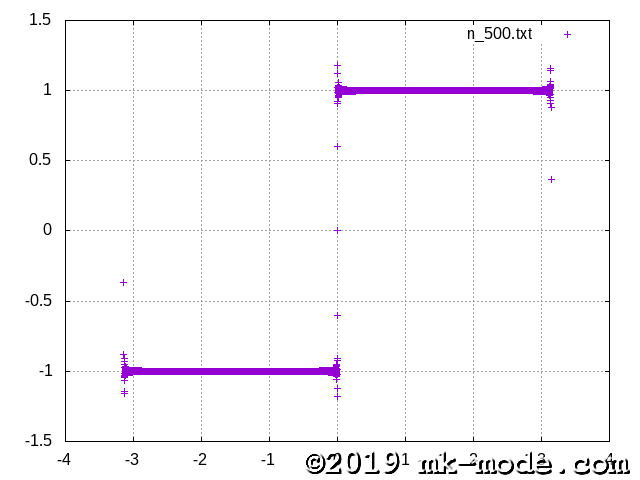
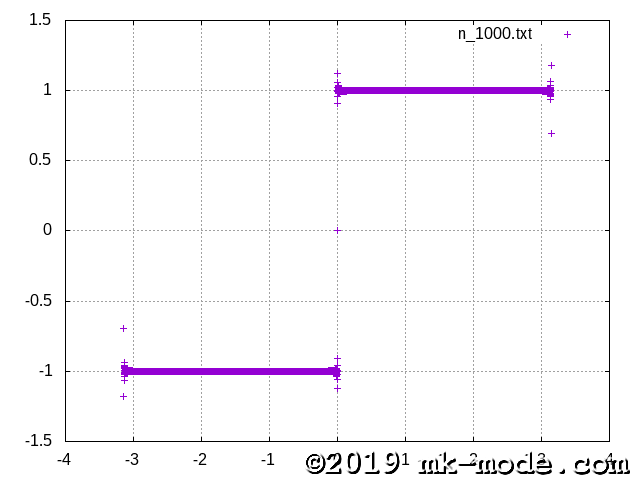
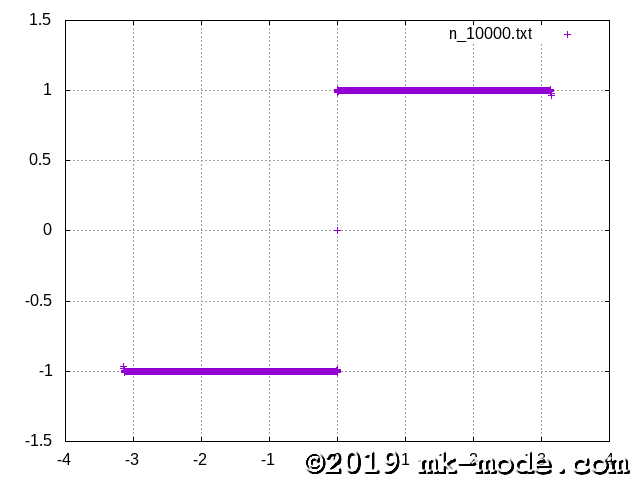
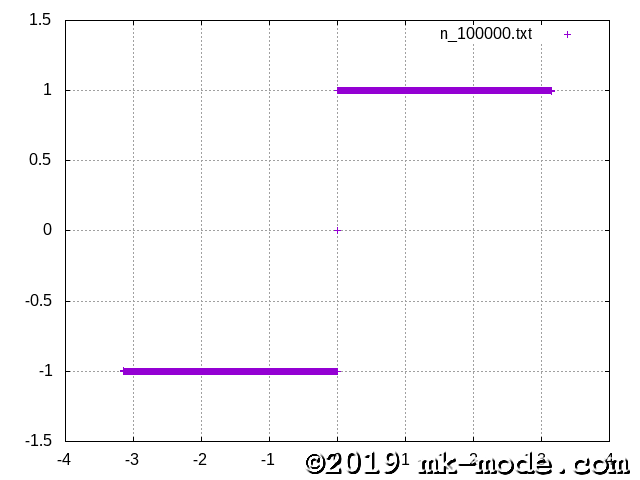
以上。

Comments