Fortran - 3次スプライン補間！

Fortran 95 で「3次スプライン補間」のアルゴリズムを実装してみました。

0. 前提条件

• LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
• GCC 6.3.0 (GFortran 6.3.0) でのコンパイルを想定。

1. アルゴリズムについて

当ブログ過去記事を参照のこと。

• Ruby - ３次スプライン補間！
• Python - ３次スプライン補間！

2. ソースコードの作成

File: spline_interpolation.f95

!****************************************************
! 3次スプライン補間
!
! * 入力はテキストファイルをパイプ処理
!     1行目:     点の数
!     2行目以降: 1行に1点(x, y)
!
!   date          name            version
!   2018.12.20    mk-mode.com     1.00 新規作成
!
! Copyright(C) 2018 mk-mode.com All Rights Reserved.
!****************************************************
!
module const
  ! SP: 単精度(4), DP: 倍精度(8)
  integer,     parameter :: SP = kind(1.0)
  integer(SP), parameter :: DP = selected_real_kind(2 * precision(1.0_SP))
end module const

module spline
  use const
  implicit none
  private
  public :: interpolate

contains
  ! 3次スプライン補間
  !
  ! :param(in) integer(4)  :: n: 点の数
  ! :param(in) real(8)  p(:, :): 点の配列
  subroutine interpolate(n, p)
    use const
    implicit none
    integer(SP), intent(in) :: n
    real(DP),    intent(in) :: p(2, n)
    real(DP) :: h(n - 1), w(n - 2), mtx(n - 1, n - 2), v(n)
    real(DP) :: a(n - 1), b(n - 1), c(n - 1), d(n)
    real(DP)    :: xp, xp_2, xp_3, x, y
    integer(SP) :: idx, i

    ! 初期計算
    h = calc_h(n, p)
    w = calc_w(n, p, h)
    call gen_mtx(n, h, w, mtx)
    call gauss_jordan(n, mtx, v)
    v = cshift(v, -1)
    b = calc_b(n, v)
    a = calc_a(n, v, p)
    d = calc_d(n, p)
    c = calc_c(n, v, p)

    ! 補間
    do i = int(p(1, 1) * 10), int(p(1, n) * 10)
      x = i * 0.1_DP
      idx = find_idx(n, p, x)
      xp   = x - p(1, idx)
      xp_2 = xp * xp
      xp_3 = xp_2 * xp
      y = a(idx) * xp_3 + b(idx) * xp_2 + c(idx) * xp + d(idx)
      print '(F8.4, X, F8.4)', x, y
    end do
  end subroutine interpolate

  ! h 計算
  !
  ! :param(in) integer(4)     n: 点の数
  ! :param(in) real(8)  p(2, n): 点の配列
  ! :return    real(8) h(n - 1): h の配列
  function calc_h(n, p) result(h)
    implicit none
    integer(SP), intent(in) :: n
    real(DP),    intent(in) :: p(2, n)
    real(DP) :: h(n - 1)

    h = p(1, 2:n) - p(1, 1:n-1)
  end function calc_h

  ! w 計算
  !
  ! :param(in) integer(4)     n: 点の数
  ! :param(in) real(8)  p(2, n): 点の配列
  ! :param(in) real(8) h(n - 1): h の配列
  ! :return    real(8) w(n - 2): w の配列
  function calc_w(n, p, h) result(w)
    implicit none
    integer(SP), intent(in) :: n
    real(DP),    intent(in) :: p(2, n), h(n - 1)
    real(DP) :: w(n - 2)

    w = 6.0_DP * ((p(2, 3:n) - p(2, 2:n-1)) &
    & / h(2:n-1) - (p(2, 2:n-1) - p(2, 1:n-2)) / h(1:n-2))
  end function calc_w

  ! 行列生成
  !
  ! :param(in)  integer(4)             n: 点の数
  ! :param(in)  real(8)         h(n - 1): h の配列
  ! :param(in)  real(8)         w(n - 2): w の配列
  ! :param(out) real(8) mtx(n - 1, n - 2: 行列
  subroutine gen_mtx(n, h, w, mtx)
    implicit none
    integer(SP), intent(in)  :: n
    real(DP),    intent(in)  :: h(n - 1), w(n - 1)
    real(DP),    intent(out) :: mtx(n - 1, n - 2)
    integer(SP) :: i

    mtx(:, :) = 0.0_DP
    do i = 1, n - 2
      mtx(i, i)  = 2.0_DP * (h(i) + h(i + 1))
      mtx(n - 1, i) = w(i)
      if (i == 1) cycle
      mtx(i, i - 1) = h(i)
      mtx(i - 1, i) = h(i)
    end do
  end subroutine gen_mtx

  ! 連立一次方程式を解く（Gauss-Jordan 法）
  !
  ! :param(in)  integer(4)             n: 点の数
  ! :param(in)  real(8) mtx(n - 1, n - 2: 行列
  ! :param(out) real(8)             v(n): v の配列
  subroutine gauss_jordan(n, mtx, v)
    implicit none
    integer(SP), intent(in)  :: n
    real(DP),    intent(in)  :: mtx(n - 1, n - 2)
    real(DP),    intent(out) :: v(n)
    integer(SP) :: i, j
    real(DP)    :: mtx_w(n - 1, n - 2)  ! 作業用
    real(DP)    :: p, d

    mtx_w(:, :) = mtx(:, :)
    v(:) = 0.0_DP
    do j = 1, n - 2
      p = mtx_w(j, j)
      mtx_w(j:n-1, j) = mtx_w(j:n-1, j) / p
      do i = 1, n - 2
        if (i == j) cycle
        d = mtx_w(j, i)
        mtx_w(j:n-1, i) = mtx_w(j:n-1, i) - d * mtx_w(j:n-1, j)
      end do
    end do
    v(1:n-2) = mtx_w(n - 1, 1:n-2)
  end subroutine gauss_jordan

  ! a 計算
  !
  ! :param(in) integer(4)     n: 点の数
  ! :param(in) real(8)     v(n): v の配列
  ! :param(in) real(8)  p(2, n): 点の配列
  ! :return    real(8) a(n - 1): a の配列
  function calc_a(n, v, p) result(a)
    implicit none
    integer(SP), intent(in) :: n
    real(DP),    intent(in) :: v(n), p(2, n)
    real(DP) :: a(n - 1)

    a = (v(2:n) - v(1:n-1)) / (6.0_DP * (p(1, 2:n) - p(1, 1:n-1)))
  end function calc_a

  ! b 計算
  !
  ! :param(in) integer(4)     n: 点の数
  ! :param(in) real(8)     v(n): v の配列
  ! :return    real(8) b(n - 1): b の配列
  function calc_b(n, v) result(b)
    implicit none
    integer(SP), intent(in) :: n
    real(DP),    intent(in) :: v(n)
    real(DP) :: b(n - 1)

    b = v(1:n-1) / 2.0_DP
  end function calc_b

  ! c 計算
  !
  ! :param(in) integer(4)     n: 点の数
  ! :param(in) real(8)     v(n): v の配列
  ! :param(in) real(8)  p(2, n): 点の配列
  ! :return    real(8)     c(n): c の配列
  function calc_c(n, v, p) result(c)
    implicit none
    integer(SP), intent(in) :: n
    real(DP),    intent(in) :: v(n), p(2, n)
    real(DP) :: c(n - 1)

    c = (p(2, 2:n) - p(2, 1:n-1)) / (p(1, 2:n) - p(1, 1:n-1)) &
    & - (p(1, 2:n) - p(1, 1:n-1)) * (2.0_DP * v(1:n-1) + v(2:n)) &
    & / 6.0_DP
  end function calc_c

  ! d 計算
  !
  ! :param(in) integer(4)     n: 点の数
  ! :param(in) real(8)  p(2, n): 点の配列
  ! :return    real(8)     d(n): d の配列
  function calc_d(n, p) result(d)
    implicit none
    integer(SP), intent(in) :: n
    real(DP),    intent(in) :: p(2, n)
    real(DP) :: d(n)

    d = p(2, :)
  end function calc_d

  ! インデックス検索
  !
  ! :param(in) integer(4)     n: 点の数
  ! :param(in) real(8)  p(2, n): 点の配列
  ! :param(in) real(8)        x: x 値
  ! :return    integer(4)   idx: インデックス
  function find_idx(n, p, x) result(idx)
    implicit none
    integer(SP), intent(in) :: n
    real(DP),    intent(in) :: p(2, n), x
    integer(SP) :: idx
    integer(SP) :: i, j, k

    i = 1
    j = n
    do while (i < j)
      k = (i + j) / 2
      if (p(1, k) < x) then
        i = k + 1
      else
        j = k
      end if
    end do
    if (i > 1) i = i - 1
    idx = i
  end function find_idx
end module spline

program spline_interpolation
  use const
  use spline
  implicit none
  character(20), parameter :: F_SRC = "src.txt"
  integer(SP),   parameter :: UID_S = 10
  integer(SP) :: n                  ! 点の数
  real(DP), allocatable :: p(:, :)  ! 点の配列
  integer(SP) :: i, ios

  ! ファイル OPEN
  open(UID_S, file = F_SRC, status = 'old')

  ! 点の数の取得
  read(UID_S, *) n

  ! 点の配列メモリ確保
  allocate(p(2, n))

  ! 点の配列読み込み
  do i = 1, n
    read(UID_S, *) p(:, i)
  end do

  ! ファイル CLOSE
  close(UID_S)

  ! 補間
  call interpolate(n, p)

  ! 点の配列メモリ解放
  deallocate(p)

  stop
end program spline_interpolation

• Gist - Fortran 95 source code to compute 3D Spline interpolation.

3. ソースコードのコンパイル

$ gfortran -o spline_interpolation spline_interpolation.f95

4. 動作確認

あらかじめ与える点の情報はテキストファイルから取り込むようにしているので、まず、テキストファイルを作成する。（1行目：点の数、2行目以降：x, y）

File: src.txt

6
0.0 0.8
2.0 3.2
3.0 2.8
5.0 4.5
7.0 2.5
8.0 1.9

そして、実行。

$ ./spline_interpolation > res.txt

5. 結果確認

File: res.txt

  0.0000   0.8000
  0.1000   0.9861
  0.2000   1.1713
  0.3000   1.3544
  0.4000   1.5346
        :
  ===< 中略 >===
        :
  7.6000   2.0754
  7.7000   2.0275
  7.8000   1.9831
  7.9000   1.9410
  8.0000   1.9000

GNUPLOT で描画。

---

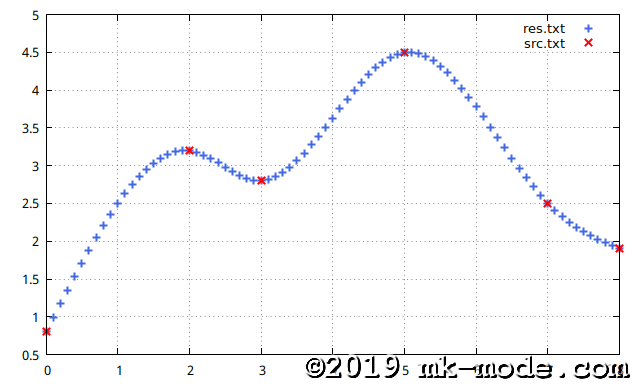
以上。