Ruby - 3次スプライン補間!
Updated:
過去に「ラグランジュ補間」や「ニュートン補間」を C++ や Ruby で実装したことがありました。
- C++ - ラグランジュ補間! - mk-mode BLOG
- Ruby - ラグランジュ補間! - mk-mode BLOG
- C++ - ニュートン補間! - mk-mode BLOG
- Ruby - ニュートン補間! - mk-mode BLOG
今回は「3次スプライン補間」を Ruby で実装してみました。
0. 前提条件
- Ruby 2.2.3-p173 での作業を想定。
- グラフも描画するので、RubyGems ライブラリの gnuplot をインストールしておく。(過去記事参照:「Ruby - gnuplot でグラフ描画!」)
1. 3次スプライン補間について
こちらの内容を自分なりに理解して以下のようにまとめた。
(数式が多いので別途 \(\LaTeX\) で記載した文書を貼り付け)
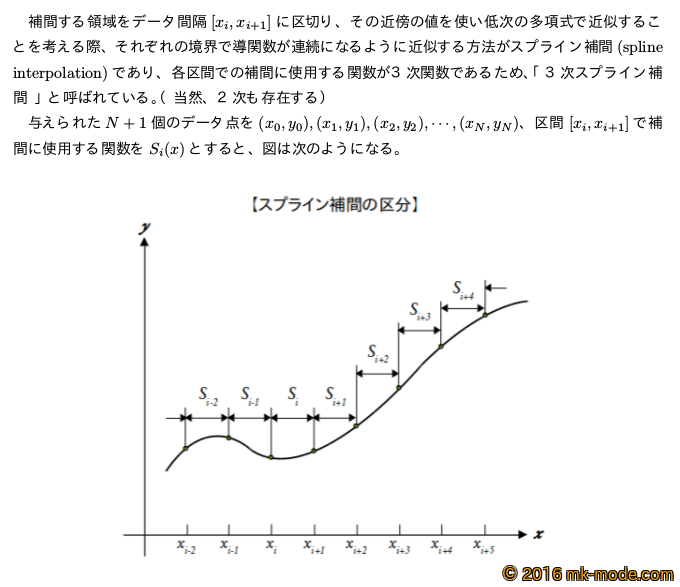





(上記文書の PDF はこちら)
2. Ruby スクリプトの作成
以下のような Ruby スクリプトを作成する。
ロジックは前項の説明(アルゴリズム)どおりなので説明しない。(ただ、連立一次方程式の解法には「ガウス・ジョルダン法」を使用した)
File: spline_interpolation.rb
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
#!/usr/local/bin/ruby
#*********************************************
# 3次スプライン補間
# (gnuplot によるグラフ描画付き)
#*********************************************
#
require 'gnuplot'
# N + 1 個の点
X = [0.0, 2.0, 3.0, 5.0, 7.0, 8.0]
Y = [0.8, 3.2, 2.8, 4.5, 2.5, 1.9]
class SplineInterpolation
def initialize
@x, @y = X, Y
@n = @x.size - 1
h = calc_h
w = calc_w(h)
matrix = gen_matrix(h, w)
v = [0, gauss_jordan(matrix), 0].flatten
@b = calc_b(v)
@a = calc_a(v)
@d = calc_d(v)
@c = calc_c(v)
end
def interpolate(t)
i = search_i(t)
return @a[i] * (t - @x[i]) ** 3 \
+ @b[i] * (t - @x[i]) ** 2 \
+ @c[i] * (t - @x[i]) \
+ @d[i]
rescue => e
$stderr.puts "[#{e.class}] #{e.message}"
exit 1
end
private
def calc_h
return (0..@n - 1).map { |i| @x[i + 1] - @x[i] }
end
def calc_w(h)
return (1..@n -1).map do |i|
6 * ((@y[i + 1] - @y[i]) / h[i] - (@y[i] - @y[i - 1]) / h[i - 1])
end
end
def gen_matrix(h, w)
matrix = Array.new(@n - 1).map { Array.new(@n, 0) }
0.upto(@n - 2) do |i|
matrix[i][i] = 2 * (h[i] + h[i + 1])
matrix[i][-1] = w[i]
next if i == 0
matrix[i - 1][i] = h[i]
matrix[i][i - 1] = h[i]
end
return matrix
end
def gauss_jordan(matrix)
v = Array.new
n = @n - 1
0.upto(n - 1) do |k|
p = matrix[k][k]
k.upto(n) { |j| matrix[k][j] /= p.to_f }
0.upto(n - 1) do |i|
next if i == k
d = matrix[i][k]
k.upto(n) { |j| matrix[i][j] -= d * matrix[k][j] }
end
end
matrix.each { |row| v << row[-1] }
return v
end
def calc_a(v)
return (0..@n - 1).map { |i| (v[i + 1] - v[i]) / (6 * (@x[i + 1] - @x[i])) }
end
def calc_b(v)
return (0..@n - 1).map { |i| v[i] / 2.0 }
end
def calc_c(v)
return (0..@n - 1).map do |i|
(@y[i + 1] - @y[i]) / (@x[i + 1] - @x[i]) \
- (@x[i + 1] - @x[i]) * (2 * v[i] + v[i + 1]) / 6
end
end
def calc_d(v)
return @y
end
def search_i(t)
i, j = 0, @x.size - 1
while i < j
k = (i + j) / 2
if @x[k] < t
i = k + 1
else
j = k
end
end
i -= 1 if i > 0
return i
end
end
class Graph
def initialize(x_g, y_g)
@x_g, @y_g, @x, @y = x_g, y_g, X, Y
end
def plot
Gnuplot.open do |gp|
Gnuplot::Plot.new(gp) do |plot|
plot.terminal "png enhanced font 'IPA P ゴシック' fontscale 1.2"
plot.output "spline_interpolation.png"
plot.title "スプライン補間"
plot.xlabel "x"
plot.ylabel "y"
plot.grid
# 計算によって得られた点
plot.data << Gnuplot::DataSet.new([@x_g, @y_g]) do |ds|
ds.with = "points"
ds.linewidth = 2
ds.linecolor = 3
ds.notitle
end
# 予め与えらた点
plot.data << Gnuplot::DataSet.new([@x, @y]) do |ds|
ds.with = "points"
ds.linewidth = 2
ds.linecolor = 1
ds.notitle
end
end
end
rescue => e
$stderr.puts "[#{e.class}] #{e.message}"
exit 1
end
end
if __FILE__ == $0
# グラフ用配列
x_g, y_g = Array.new, Array.new
# 3次スプライン補間
obj = SplineInterpolation.new
X[0].step(X[-1], 0.1) do |x|
y = obj.interpolate(x)
puts "%8.4f, %8.4f" % [x, y]
x_g << x
y_g << y
end
# グラフ描画
Graph.new(x_g, y_g).plot
end
3. Ruby スクリプトの実行
まず、実行権限を付与。
$ chmod +x spline_interpolation.rb
そして、実行。
$ ./spline_interpolation.rb
0.0000, 0.8000
0.1000, 0.9861
0.2000, 1.1713
0.3000, 1.3544
0.4000, 1.5346
0.5000, 1.7108
0.6000, 1.8820
0.7000, 2.0473
0.8000, 2.2056
0.9000, 2.3559
1.0000, 2.4973
1.1000, 2.6287
1.2000, 2.7492
1.3000, 2.8578
1.4000, 2.9534
1.5000, 3.0351
1.6000, 3.1019
1.7000, 3.1528
1.8000, 3.1868
1.9000, 3.2028
2.0000, 3.2000
2.1000, 3.1782
: :
====< 途中省略>====
: :
7.5000, 2.1279
7.6000, 2.0754
7.7000, 2.0275
7.8000, 1.9831
7.9000, 1.9410
8.0000, 1.9000
4. グラフ確認
Ruby スクリプトと同じディレクトリ内に “spline_interpolation.png” という画像ファイルが存在するはずなので、確認してみる。
(赤色の x が予め与えられた点、水色の + が補間された点)
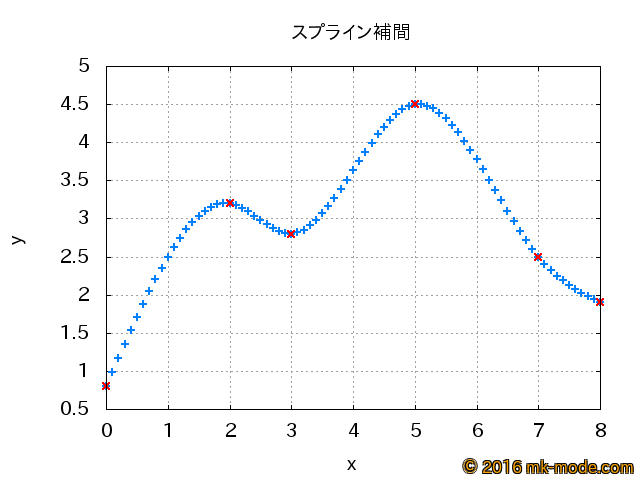
5. 参考サイト
- Ruby - 連立方程式解法(ガウス・ジョルダン法)!(当ブログ過去記事)
スプライン補間ができないと先に進めない(私的な)事案があったために今回まとめてみた次第です。
以上。

Comments