Ruby - 単回帰分析(2次曲線回帰)の決定係数計算!
Updated:
Ruby で2つの単回帰分析(2次曲線回帰)の決定係数を計算してみました。
単回帰曲線(2次)の計算は Array クラスを拡張して行なっています。
0. 前提条件
- LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
- Ruby 2.6.3 での作業を想定。
1. 決定係数について
前回記事を参照。
2. Ruby スクリプトの作成
- 以下のスクリプトでは2種の方法で決定係数を計算している。
- Shebang ストリング(1行目)では、フルパスでコマンド指定している。(当方の慣習)
File: coefficient_of_determination_2d.rb
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
#! /usr/local/bin/ruby
#*********************************************************
# Ruby script to calculate a coefficient of determination.
#*********************************************************
#
class CoefficientOfDetermination
# 説明変数と目的変数
X = [83, 71, 64, 69, 69, 64, 68, 59, 81, 91, 57, 65, 58, 62]
Y = [183, 168, 171, 178, 176, 172, 165, 158, 183, 182, 163, 175, 164, 175]
# Execution
def exec
puts "説明変数 X = {#{X.join(', ')}}"
puts "目的変数 Y = {#{Y.join(', ')}}"
puts "---"
# 単回帰曲線算出
reg_curve = X.reg_curve(Y)
puts " a = %20.16f" % reg_curve[:a]
puts " b = %20.16f" % reg_curve[:b]
puts " c = %20.16f" % reg_curve[:c]
# 推定値
y_e = calc_estimations(X, reg_curve[:a], reg_curve[:b], reg_curve[:c])
# 標本値 Y (目的変数)の平均
y_b = Y.inject(0) { |s, a| s += a } / Y.size.to_f
puts "決定係数"
# 解法-1. 決定係数 (= 推定値の変動 / 標本値の変動)
r_2 = calc_s_r(y_b, y_e) / calc_s_y2(y_b, Y)
puts " R2 (1) = %20.16f" % r_2
# 解法-2. 決定係数 (= 1 - 残差の変動 / 標本値の変動)
r_2 = 1.0 - calc_s_e(Y, y_e) / calc_s_y2(y_b, Y)
puts " R2 (2) = %20.16f" % r_2
rescue => e
$stderr.puts "[#{e.class}] #{e.message}"
e.backtrace.each{ |tr| $stderr.puts "\t#{tr}" }
exit 1
end
private
# 推定値
#
# @param xs: 説明変数配列
# @param a: 回帰曲線の a
# @param b: 回帰曲線の b
# @param b: 回帰曲線の c
# @return y_e: 推定値配列
def calc_estimations(xs, a, b, c)
y_e = Array.new
begin
xs.each { |x| y_e << a + b * x + c * x * x }
return y_e
rescue => e
raise
end
end
# 推定値の変動
#
# @param y_b: 標本値(目的変数)の平均
# @param y_e: 推定値配列
# @return s_r: 推定値の変動
def calc_s_r(y_b, y_e)
s_r = 0.0
begin
y_e.each do |a|
v = a - y_b
s_r += v * v
end
return s_r
rescue => e
raise
end
end
# 標本値の変動
#
# @param y_b: 標本値(目的変数)の平均
# @param y_s: 標本値(目的変数)配列
# @return s_y2: 標本値の変動
def calc_s_y2(y_b, y_s)
s_y2 = 0.0
begin
y_s.each do |a|
v = a - y_b
s_y2 += v * v
end
return s_y2
rescue => e
raise
end
end
# 残差の変動
#
# @param y_s: 標本値(目的変数)配列
# @param y_e: 推定値配列
# @return s_e: 残差の変動
def calc_s_e(y_s, y_e)
s_e = 0.0
begin
y_s.zip(y_e).each do |a, b|
v = a - b
s_e += v * v
end
return s_e
rescue => e
raise
end
end
end
class Array
# 単回帰曲線(2次)
def reg_curve(y)
# 以下の場合は例外スロー
# - 引数の配列が Array クラスでない
# - 自身配列が空
# - 配列サイズが異なれば例外
raise "Argument is not a Array class!" unless y.class == Array
raise "Self array is nil!" if self.size == 0
raise "Argument array size is invalid!" unless self.size == y.size
n = self.size # number of items
m_x = self.sum / n.to_f # avg(X)
m_y = y.sum / n.to_f # avg(Y)
m_x2 = self.map { |x| x ** 2 }.sum / n.to_f # avg(X^2)
m_x3 = self.map { |x| x ** 3 }.sum / n.to_f # avg(X^3)
m_x4 = self.map { |x| x ** 4 }.sum / n.to_f # avg(X^4)
m_xy = self.zip(y).map { |a, b| a * b }.sum / n.to_f # avg(X * Y)
m_x2y = self.zip(y).map { |a, b| a * a * b }.sum / n.to_f # avg(X^2 * Y)
s_xx = m_x2 - m_x * m_x # Sxx
s_xy = m_xy - m_x * m_y # Sxy
s_xx2 = m_x3 - m_x * m_x2 # Sxx2
s_x2x2 = m_x4 - m_x2 * m_x2 # Sx2x2
s_x2y = m_x2y - m_x2 * m_y # Sx2y
b = s_xy * s_x2x2 - s_x2y * s_xx2
b /= s_xx * s_x2x2 - s_xx2 * s_xx2
c = s_x2y * s_xx - s_xy * s_xx2
c /= s_xx * s_x2x2 - s_xx2 * s_xx2
a = m_y - b * m_x - c * m_x2
{a: a, b: b, c: c}
end
end
CoefficientOfDetermination.new.exec if __FILE__ == $0
4. Ruby スクリプトの実行
$ ./coefficient_of_determination_2d.rb
説明変数 X = {83, 71, 64, 69, 69, 64, 68, 59, 81, 91, 57, 65, 58, 62}
目的変数 Y = {183, 168, 171, 178, 176, 172, 165, 158, 183, 182, 163, 175,164, 175}
---
a = 41.3745396407205561
b = 3.0867232029882175
c = -0.0168356480763719
決定係数
R2 (1) = 0.6664619960148396
R2 (2) = 0.6664619960150644
決定係数が 約0.67 となっているので、2次回帰曲線の当てはまりはやや良いと言える。
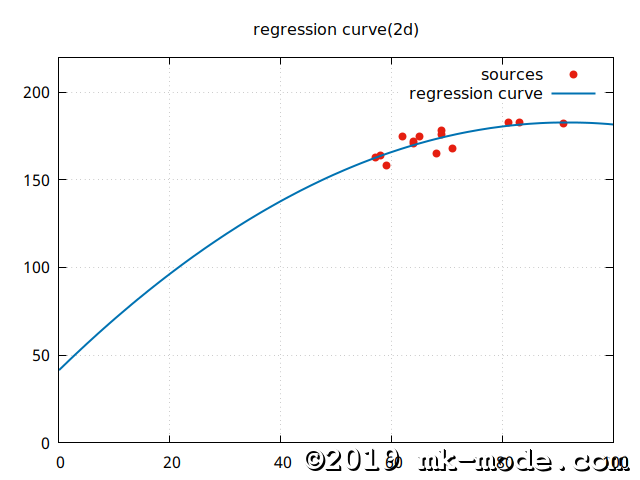
5. 視覚的な確認
参考までに、上記スクリプトで使用した2変量の各点と作成された2次回帰曲線を gnuplot で描画してみた。
以上。

Comments