Fortran - 2つの配列から単回帰曲線(指数(ab指数)回帰モデル)計算!
Updated:
Fortran 95 で、数値からなる同サイズの配列2つを説明変数・目的変数とみなして単回帰曲線(指数(ab指数)回帰モデル)を計算してみました。(連立方程式の解法にはガウスの消去法を使用)
0. 前提条件
- LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
- GCC 6.3.0 (GFortran 6.3.0) でのコンパイルを想定。
1. 単回帰曲線(指数(ab指数)回帰モデル)の求め方
求める曲線を \(y=ab^x\) とする。両辺自然対数をとると
\(\log{y} = \log{ab^x}\) で、さらに \(\log{y}=\log{a} + x\log{b}\) と変形できる。
(ここでの \(\log\) は自然対数 \(\log_e\) のことである)
そして、残差の二乗和 \(S\) は
となる。 \(a,b\) それぞれで偏微分したものを \(0\) とする。
\[\begin{eqnarray*} \frac{\partial S}{\partial a} &=& \frac{2}{a}\sum_{i=1}^{N}(\log{a}+x_{i}\log{b} - \log{y_i})= 0 \\ \frac{\partial S}{\partial b} &=& \frac{2}{b}\sum_{i=1}^{N}(\log{a}+x_{i}\log{b} - \log{y_i})x_i= 0 \end{eqnarray*}\]\(\log{a} = A, \ \log{b} = B\) とおいて、これらを変形すると、
\[\begin{eqnarray*} AN + B\sum_{i=1}^{N}x_i &=& \sum_{i=1}^{N}\log{y_i} \\ A\sum_{i=1}^{N}x_i + B\sum_{i=1}^{N}x_i^2 &=& \sum_{i=1}^{N}x_{i}\log{y_i } \end{eqnarray*}\]となる。これらの連立方程式を解いて、 \(A,\ B\) を得る。
\(\log{a} = A, \ \log{b} = B\) より \(a=e^A, \ b=e^B\) であることから、 \(a,\ b\) が求まる。
2. ガウスの消去法による連立方程式の解法について
当ブログ過去記事を参照。
3. ソースコードの作成
File: regression_curve_exp.f95
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
!****************************************************
! 単回帰曲線(指数(ab指数)回帰)計算
! : y = a * b**x
! : 連立方程式は ガウスの消去法で解く
!
! date name version
! 2019.04.10 mk-mode.com 1.00 新規作成
!
! Copyright(C) 2019 mk-mode.com All Rights Reserved.
!****************************************************
!
module const
! SP: 単精度(4), DP: 倍精度(8)
integer, parameter :: SP = kind(1.0)
integer(SP), parameter :: DP = selected_real_kind(2 * precision(1.0_SP))
end module const
module comp
use const
implicit none
private
public :: calc_reg_curve_exp
contains
! 単回帰曲線(指数(ab指数)回帰)計算
!
! :param(in) real(8) x(:): 説明変数配列
! :param(in) real(8) y(:): 目的変数配列
! :param(out) real(8) a: 係数 a
! :param(out) real(8) b: 係数 b
subroutine calc_reg_curve_exp(x, y, a, b)
implicit none
real(DP), intent(in) :: x(:), y(:)
real(DP), intent(out) :: a, b
integer(SP) :: size_x, size_y, i
real(DP) :: sum_x, sum_x2, sum_ly, sum_xly
real(DP) :: mtx(2, 3)
real(DP), allocatable :: ly(:)
size_x = size(x)
size_y = size(y)
if (size_x == 0 .or. size_y == 0) then
print *, "[ERROR] array size == 0"
stop
end if
if (size_x /= size_y) then
print *, "[ERROR] size(X) != size(Y)"
stop
end if
allocate(ly(size_y))
ly = log(y)
sum_x = sum(x)
sum_x2 = sum(x * x)
sum_ly = sum(ly)
sum_xly = sum(x * ly)
deallocate(ly)
mtx(1, :) = (/real(size_x, DP), sum_x, sum_ly/)
mtx(2, :) = (/ sum_x, sum_x2, sum_xly/)
call solve_ge(2, mtx)
a = exp(mtx(1, 3))
b = exp(mtx(2, 3))
end subroutine calc_reg_curve_exp
! 連立方程式を解く(ガウスの消去法)
!
! :param(in) integer(4) n: 元数
! :param(inout) real(8) a(n,n+1): 係数配列
subroutine solve_ge(n, a)
implicit none
integer(SP), intent(in) :: n
real(DP), intent(inout) :: a(n, n + 1)
integer(SP) :: i, j
real(DP) :: d
! 前進消去
do j = 1, n - 1
do i = j + 1, n
d = a(i, j) / a(j, j)
a(i, j+1:n+1) = a(i, j+1:n+1) - a(j, j+1:n+1) * d
end do
end do
! 後退代入
do i = n, 1, -1
d = a(i, n + 1)
do j = i + 1, n
d = d - a(i, j) * a(j, n + 1)
end do
a(i, n + 1) = d / a(i, i)
end do
end subroutine solve_ge
end module comp
program regression_curve_exp
use const
use comp
implicit none
character(9), parameter :: F_INP = "input.txt"
integer(SP), parameter :: UID = 10
real(DP) :: a, b
integer(SP) :: n, i
character(20) :: f
real(DP), allocatable :: x(:), y(:)
! IN ファイル OPEN
open(UID, file = F_INP, status = "old")
! データ数読み込み
read(UID, *) n
! 配列用メモリ確保
allocate(x(n))
allocate(y(n))
! データ読み込み
do i = 1, n
read(UID, *) x(i), y(i)
end do
write(f, '("(A, ", I0, "F8.2, A)")') n
print f, "説明変数 X = (", x, ")"
print f, "目的変数 Y = (", y, ")"
print '(A)', "---"
! IN ファイル CLOSE
close (UID)
! 回帰曲線計算
call calc_reg_curve_exp(x, y, a, b)
print '(A, F12.8)', "a = ", a
print '(A, F12.8)', "b = ", b
! 配列用メモリ解放
deallocate(x)
deallocate(y)
stop
end program regression_curve_exp
4. ソースコードのコンパイル
$ gfortran -o regression_curve_exp regression_curve_exp.f95
5. 動作確認
まず、以下のような入力ファイルを用意する。
(先頭行:点の数、2行目以降:各点)
File: input.txt
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14
83 183
71 168
64 171
69 178
69 176
64 172
68 165
59 158
81 183
91 182
57 163
65 175
58 164
62 175
そして、実行。
$ ./regression_curve_exp
説明変数 X = ( 83.00 71.00 64.00 69.00 69.00 64.00 68.00 59.00 81.00 91.00 57.00 65.00 58.00 62.00)
目的変数 Y = ( 183.00 168.00 171.00 178.00 176.00 172.00 165.00 158.00 183.00 182.00 163.00 175.00 164.00 175.00)
---
a = 134.44579219
b = 1.00361092
6. 視覚的な確認
参考までに、上記スクリプトで使用した2変量の各点と作成された単回帰曲線を gnuplot で描画してみた。
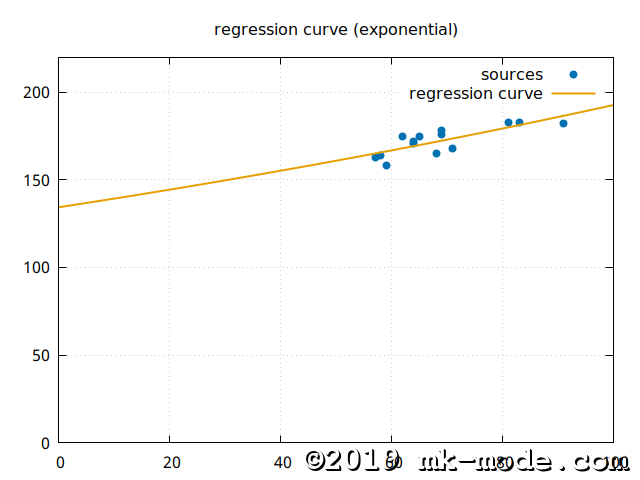
以上。

Comments