mk-mode.com

mk-mode.com

Linux, Debian, IT, Server, PG, Ruby, Rails, Python, C++, Fortran, PC, MariaDB, math, GIS, etc...

C++ - 単回帰分析（2次曲線回帰）の決定係数計算！

Updated:


C++ で単回帰分析（2次曲線回帰）の決定係数を計算してみました。

過去には Fortran 等で実装しています。

0. 前提条件

  • Debian GNU/Linux 10.3 (64bit) での作業を想定。
  • GCC 9.2.0 (G++ 9.2.0) (C++17) でのコンパイルを想定。

1. 決定係数について

回帰分析において、目的変数の標本値（実測値）に対する目的変数の推測値（予測値）の説明力を表す指標（言い換えれば、説明変数（独立変数）が目的変数（従属変数）をどれくらい説明できているかを表す統計量）が

\[\begin{eqnarray*} 決定係数 R^2 \end{eqnarray*}\]

である。（「\(R\)の\(2\)乗」で表現するが、必ずしも何かの値の \(2\) 乗になるという意味ではない）

決定係数 \(R^2\) は次のように定義する。（定義の仕方は複数あるが、次の定義が最も一般的）

\[\begin{eqnarray*} 決定係数 R^2 = \frac{推定値の変動}{標本値の変動} = \frac{S_R}{S_{y^2}} \end{eqnarray*}\]

但し、

\[\begin{eqnarray*} 標本値の変動 &=& \sum_{i=1}^{N}(y_i - \bar{y})^2 = S_{y^2} \\ 推定値の変動 &=& \sum_{i=1}^{N}(Y_i - \bar{y})^2 = S_R \\ 残差の変動 &=& \sum_{i=1}^{N}(y_i - Y_i)^2 = S_E \end{eqnarray*}\]

これら3つの変動の間には次のような関係が成り立つ。

\[\begin{eqnarray*} 標本値の変動 = 推定値の変動 + 残差の変動 \end{eqnarray*}\]

これから、

\[\begin{eqnarray*} 1 &=& \frac{推定値の変動}{標本値の変動} + \frac{残差の変動}{標本値の変動} \\ \therefore \ \ 1 &=& 決定係数 R^2 + \frac{残差の変動}{標本値の変動} \\ \end{eqnarray*}\]

よって、

\[\begin{eqnarray*} 決定係数 R^2 &=& 1 - \frac{残差の変動}{標本値の変動} \end{eqnarray*}\]

となる。これは、「残差の変動が \(0\) に近ければ、決定係数が \(1\) が近くなる」ということで、「決定係数 \(R^2\) が \(1\) に近いほど、当てはまりが良い（説明変数が目的変数をより説明できている）」と表現できることになる。

ちなみに、単回帰分析（線形回帰）の場合、

\[\begin{eqnarray*} (xとyの相関係数)^2 = 決定係数 \end{eqnarray*}\]

となる。また、

\[\begin{eqnarray*} S_{y^2} &=& \sum_{i=1}^{N}y_i^2 - \frac{\left( \displaystyle{\sum_{i=1}^{N}y_i} \right)^2}{N} \\ S_{xy} &=& \sum_{i=1}^{N}x_{i}y_{i} - \frac{\displaystyle{\sum_{i=1}^{N}x_i} \sum_{i=1}^{N}y_i}{N} \\ S_R &=& b \cdot S_{xy} \\ \end{eqnarray*}\]

でるあること（導出方法は略）を利用して、 \(\begin{eqnarray*} 決定係数 R^2 &=& \frac{S_R}{S_{y^2}} \end{eqnarray*}\)

を求めることもできる。

2. ソースコードの作成

  • 以下のソースコードでは4種の方法で決定係数を計算している。
  • ファイル読み込み部分、計算部分、実行部分とソースファイルを分けている。

File: file.hpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

#ifndef COEFFICIENT_OF_DETERMINATION_2D_FILE_HPP_
#define COEFFICIENT_OF_DETERMINATION_2D_FILE_HPP_

#include <fstream>
#include <string>
#include <vector>

class File {
  std::string f_data;

public:
  File(std::string f_data) : f_data(f_data) {}
  bool get_text(std::vector<std::vector<double>>&);
};

#endif

File: file.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

#include "file.hpp"

#include <iostream>
#include <sstream>
#include <string>
#include <vector>

bool File::get_text(std::vector<std::vector<double>>& data) {
  try {
    // ファイル OPEN
    std::ifstream ifs(f_data);
    if (!ifs.is_open()) return false;  // 読み込み失敗

    // ファイル READ
    std::string buf;                   // 1行分バッファ
    while (getline(ifs, buf)) {
      std::vector<double> rec;         // 1行分ベクタ
      std::istringstream iss(buf);     // 文字列ストリーム
      std::string field;               // 1列分文字列

      // 1行分文字列を1行分ベクタに追加
      double x, y;
      while (iss >> x >> y) {
        rec.push_back(x);
        rec.push_back(y);
      }

      // １行分ベクタを data ベクタに追加
      if (rec.size() != 0) data.push_back(rec);
    }
  } catch (...) {
      std::cerr << "EXCEPTION!" << std::endl;
      return false;
  }

  return true;  // 読み込み成功
}

File: calc.hpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#ifndef COEFFICIENT_OF_DETERMINATION_2D_CALC_HPP_
#define COEFFICIENT_OF_DETERMINATION_2D_CALC_HPP_

#include <vector>

class Calc {
  std::vector<std::vector<double>> data;             // 元データ
  std::vector<std::vector<double>> mtx;              // 計算用行列
  bool solve_ge(std::vector<std::vector<double>>&);  // ガウスの消去法

public:
  Calc(std::vector<std::vector<double>>& data) : data(data) {
    cnt = data.size();
  }
  unsigned int cnt;                                        // データ件数
  bool reg_curve_2d(double&, double&, double&);            // 単回帰直線の計算
  bool y_e(double, double, double, std::vector<double>&);  // 計算・推定値
  double y_b();                                            // 計算・標本値 Y (目的変数)の平均
  double s_r(std::vector<double>, double);                 // 計算・推定値の変動
  double s_y2(double);                                     // 計算・標本値の変動
  double s_e(std::vector<double>);                         // 計算・残渣の変動
  double r_2(double);                                      // 計算・決定係数（公式使用）
};

#endif

File: calc.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233

#include "calc.hpp"

#include <cmath>
#include <iostream>
#include <sstream>
#include <vector>

/**
 * @brief      単回帰曲線（2次）の計算
 *
 * @param[ref] a (double)
 * @param[ref] b (double)
 * @param[ref] c (double)
 * @return     真偽(bool)
 * @retval     true  成功
 * @retval     false 失敗
 */
bool Calc::reg_curve_2d(double& a, double& b, double& c) {
  unsigned int i;     // loop インデックス
  double s_x   = 0.0;  // sum(x)
  double s_x2  = 0.0;  // sum(xx)
  double s_x3  = 0.0;  // sum(xxx)
  double s_x4  = 0.0;  // sum(xxxx)
  double s_y   = 0.0;  // sum(y)
  double s_xy  = 0.0;  // sum(xy)
  double s_x2y = 0.0;  // sum(xxy)
  double x     = 0.0;  // x    計算用
  double x2    = 0.0;  // xx   計算用
  double x3    = 0.0;  // xxx  計算用
  double x4    = 0.0;  // xxxx 計算用
  double y     = 0.0;  // y    計算用

  try {
    // データ数
    cnt = data.size();

    // sum(x), sum(xx), sum(xxx), sum(xxxx),
    // sum(y), sum(xx), sum(xy), sum(x2y)
    for (i = 0; i < cnt; i++) {
      x  = data[i][0];
      y  = data[i][1];
      x2 = x  * x;
      x3 = x2 * x;
      x4 = x3 * x;
      s_x   += x;
      s_x2  += x2;
      s_x3  += x3;
      s_x4  += x4;
      s_y   += y;
      s_xy  += x  * y;
      s_x2y += x2 * y;
    }
    // 行列1行目
    mtx.push_back({(double)cnt, s_x, s_x2, s_y});
    // 行列2行目
    mtx.push_back({s_x, s_x2, s_x3, s_xy});
    // 行列3行目
    mtx.push_back({s_x2, s_x3, s_x4, s_x2y});

    // 計算（ガウスの消去法）
    if (!solve_ge(mtx)) {
      std::cout << "[ERROR] Failed to solve by the Gauss-Ellimination method!"
                << std::endl;
      return false;
    }

    // a, b, c
    a = mtx[0][3];
    b = mtx[1][3];
    c = mtx[2][3];
  } catch (...) {
    return false;  // 計算失敗
  }

  return true;  // 計算成功
}

/**
 * @brief      ガウスの消去法
 *
 * @param[ref] 行列（配列） mtx (double)
 * @return     真偽             (bool)
 * @retval     true  成功
 * @retval     false 失敗
 */
bool Calc::solve_ge(std::vector<std::vector<double>>& mtx) {
  int i;     // loop インデックス
  int j;     // loop インデックス
  int k;     // loop インデックス
  int n;     // 元（行）の数
  double d;  // 計算用

  try {
    n = (int)mtx.size();

    // 前進消去
    for (k = 0; k < n - 1; k++) {
      for (i = k + 1; i < n; i++) {
        d = mtx[i][k] / mtx[k][k];
        for (j = k + 1; j <= n; j++)
          mtx[i][j] -= mtx[k][j] * d;
      }
    }

    // 後退代入
    for (i = n - 1; i >= 0; i--) {
      d = mtx[i][n];
      for (j = i + 1; j < n; j++)
        d -= mtx[i][j] * mtx[j][n];
      mtx[i][n] = d / mtx[i][i];
    }
  } catch (...) {
    return false;  // 計算失敗
  }

  return true;  // 計算成功
}

/**
 * @brief      計算・推定値
 *             (y_e = a + b * x)
 *
 * @param      切片     a (double)
 * @param      傾き     b (double)
 * @param[ref] 推定値 y_e (vector<double>)
 * @return     真偽       (bool)
 * @retval     true  成功
 * @retval     false 失敗
 */
bool Calc::y_e(
  double a, double b, double c,
  std::vector<double>& y_e
) {
  unsigned int i;     // loop インデックス

  try {
    for (i = 0; i < cnt; i++)
      y_e.push_back(a + (b + c * data[i][0]) * data[i][0]);
  } catch (...) {
    return false;  // 計算失敗
  }

  return true;  // 計算成功
}

/**
 * @brief      計算・標本値 Y (目的変数)の平均
 *             (y_b = sum(y) / size(y))
 *
 * @return     標本値 Y (目的変数)の平均 (double)
 */
double Calc::y_b() {
  unsigned int i;     // loop インデックス
  double s = 0.0;

  try {
    for (i = 0; i < cnt; i++)
      s += data[i][1];
    return s / cnt;
  } catch (...) {
    throw;
  }
}

/**
 * @brief      計算・推定値の変動
 *             (sum((y_e - y_b)**2))
 *
 * @param      推定値          y_e (vector<double>)
 * @param      標本値 Y の平均 y_b (double)
 * @return     推定値の変動        (double)
 */
double Calc::s_r(std::vector<double> y_e, double y_b) {
  unsigned int i;     // loop インデックス
  double v = 0.0;
  double s = 0.0;

  try {
    for (i = 0; i < cnt; i++) {
      v = y_e[i] - y_b;
      s += v * v;
    }
    return s;
  } catch (...) {
    throw;
  }
}

/**
 * @brief      計算・標本値の変動
 *             (sum((y - y_b)**2))
 *
 * @param      標本値 Y の平均 y_b (double)
 * @return     標本値の変動        (double)
 */
double Calc::s_y2(double y_b) {
  unsigned int i;     // loop インデックス
  double v = 0.0;
  double s = 0.0;

  try {
    for (i = 0; i < cnt; i++) {
      v = data[i][1] - y_b;
      s += v * v;
    }
    return s;
  } catch (...) {
    throw;
  }
}

/**
 * @brief      計算・残渣の変動
 *             (sum((y - y_e)**2))
 *
 * @param      推定値  y_b (vector<double>)
 * @return     残渣の変動  (double)
 */
double Calc::s_e(std::vector<double> y_e) {
  unsigned int i;     // loop インデックス
  double v = 0.0;
  double s = 0.0;

  try {
    for (i = 0; i < cnt; i++) {
      v = data[i][1] - y_e[i];
      s += v * v;
    }
    return s;
  } catch (...) {
    throw;
  }
}

File: coefficient_of_determination_2d.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101

/***********************************************************
  単回帰分析（2次曲線回帰）決定係数計算
  : y = a + b * x + c * x^2
  : 連立方程式をガウスの消去法で解く方法

    DATE          AUTHOR          VERSION
    2020.06.28    mk-mode.com     1.00 新規作成

  Copyright(C) 2020 mk-mode.com All Rights Reserved.
***********************************************************/
#include "calc.hpp"
#include "file.hpp"

#include <cstdlib>   // for EXIT_XXXX
#include <iomanip>   // for setprecision
#include <iostream>
#include <string>
#include <vector>

int main(int argc, char* argv[]) {
  std::string f_data;                     // データファイル名
  std::vector<std::vector<double>> data;  // データ配列
  std::size_t i;                          // loop インデックス
  double a;                               // 定数 a
  double b;                               // 係数 b
  double c;                               // 係数 c
  std::vector<double> y_e;                // 推定値
  double y_b;                             // 標本値 Y （目的変数）の平均
  double s_r;                             // 推定値の変動
  double s_y2;                            // 標本値の変動
  double s_e;                             // 残差の変動

  try {
    // === コマンドライン引数のチェック
    if (argc != 2) {
      std::cerr << "[ERROR] Number of arguments is wrong!\n"
                << "[USAGE] ./coefficient_of_determination_2d <file_name>"
                << std::endl;
      return EXIT_FAILURE;
    }

    // === ファイル名取得
    f_data = argv[1];

    // === データ取得
    File file(f_data);
    if (!file.get_text(data)) {
      std::cout << "[ERROR] Failed to read the file!" << std::endl;
      return EXIT_FAILURE;
    }
    std::cout << std::fixed << std::setprecision(4);
    std::cout << "説明変数 X  目的変数 Y" << std::endl;
    for (i = 0; i < data.size(); i++)
      std::cout << std::setw(10) << std::right << data[i][0]
                << "  "
                << std::setw(10) << std::right << data[i][1]
                << std::endl;

    // === 計算（線形回帰）
    Calc calc(data);
    if (!calc.reg_curve_2d(a, b, c)) {
      std::cout << "[ERROR] Failed to calculate!" << std::endl;
      return EXIT_FAILURE;
    }
    std::cout << std::fixed << std::setprecision(8);
    std::cout << "---\n"
              << "    a = " << std::setw(16) << std::right << a
              << "\n"
              << "    b = " << std::setw(16) << std::right << b
              << "\n"
              << "    c = " << std::setw(16) << std::right << c
              << std::endl;

    // === 計算（決定係数）
    // 推定値
    if (!calc.y_e(a, b, c, y_e)) {
      std::cout << "[ERROR] Failed to calculate!" << std::endl;
      return EXIT_FAILURE;
    }
    // 標本値 Y （目的変数）の平均
    y_b  = calc.y_b();
    // 推定値の変動
    s_r  = calc.s_r(y_e, y_b);
    // 標本値の変動
    s_y2 = calc.s_y2(y_b);
    // 残差の変動
    s_e  = calc.s_e(y_e);
    std::cout << "---" << std::endl;
    // 解法-1. 決定係数 (= 推定値の変動 / 標本値の変動)
    std::cout << "    R2 (1) = " << std::setprecision(16) << std::right
              << s_r / s_y2 << std::endl;
    // 解法-2. 決定係数 (= 1 - 残差の変動 / 標本値の変動)
    std::cout << "    R2 (2) = " << std::setprecision(16) << std::right
              << 1.0 - s_e / s_y2 << std::endl;
  } catch (...) {
      std::cerr << "EXCEPTION!" << std::endl;
      return EXIT_FAILURE;
  }

  return EXIT_SUCCESS;
}

3. ソースコードのコンパイル

まず、以下のように Makefile を作成する。（行頭のインデントはタブ文字）

File: Makefile

gcc_options = -std=c++17 -Wall -O2 --pedantic-errors

coefficient_of_determination_2d: coefficient_of_determination_2d.o file.o calc.o
	g++ $(gcc_options) -o $@ $^

coefficient_of_determination_2d.o : coefficient_of_determination_2d.cpp
	g++ $(gcc_options) -c $<

file.o : file.cpp
	g++ $(gcc_options) -c $<

calc.o : calc.cpp
	g++ $(gcc_options) -c $<

run : coefficient_of_determination_2d
	./coefficient_of_determination_2d

clean :
	rm -f ./coefficient_of_determination_2d
	rm -f ./*.o

.PHONY : run clean

そして、ビルド（コンパイル＆リンク）。

$ make

4. 動作確認

まず、以下のような入力ファイルを用意する。
（各行は x と y の値）

File: data.txt

1
2
3
4
5
6
7
8
9
10
11
12
13
14

83 183
71 168
64 171
69 178
69 176
64 172
68 165
59 158
81 183
91 182
57 163
65 175
58 164
62 175

そして、ファイル名を引数に指定して実行。

$ ./coefficient_of_determination_2d data.txt
説明変数 X  目的変数 Y
   83.0000    183.0000
   71.0000    168.0000
   64.0000    171.0000
   69.0000    178.0000
   69.0000    176.0000
   64.0000    172.0000
   68.0000    165.0000
   59.0000    158.0000
   81.0000    183.0000
   91.0000    182.0000
   57.0000    163.0000
   65.0000    175.0000
   58.0000    164.0000
   62.0000    175.0000
---
    a =      41.37453964
    b =       3.08672320
    c =      -0.01683565
---
    R2 (1) = 0.6664619960150091
    R2 (2) = 0.6664619960150633

参考までに、上記で使用した2変量の各点と作成された単回帰直線を gnuplot で描画してみた。

REGRESSION_CURVE_2D

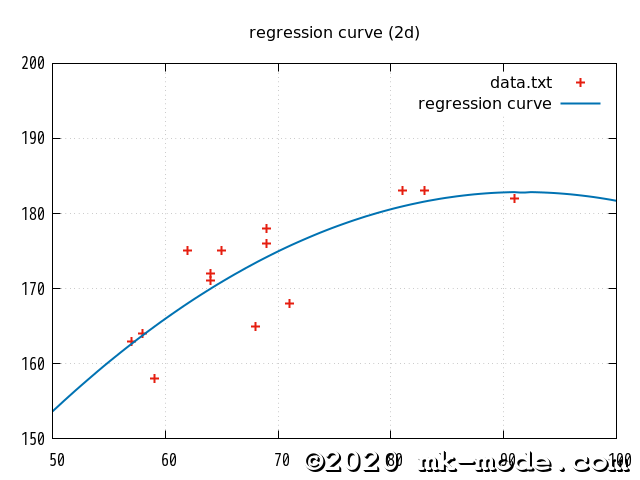
以上。





 

Sponsored Link

 

Comments

You May Also Enjoy

Debian 12 (bookworm) - Ruby 3.3 インストール（ソースビルド）！  (2024-05-18)

Debian GNU/Linux 12 (bookworm) に Ruby 3.3 をソースをビルドしてインストール方法についての記録です。 以前古いバージョンでの作業時に残していた記録を参考に作業を行い、今回更新した作業記録を貼付する形式の内容となっています。 （当然ながら、興味がなければスルーしてください）