Ruby - ロジスティック回帰分析！

2か月ほど前、説明変数K個・目的変数1個のロジスティック回帰分析のアルゴリズムをプログラムとして実装できるようにするために自分なりに理解してまとめたものを紹介しました。

• ロジスティック回帰分析！

今回は、そのアルゴリズムを Ruby で実装してみました。（但し、行列計算では matrix ライブラリを使用）

0. 前提条件

• Debian GNU/Linux 11.5 での作業を想定。
• Ruby 3.1.2 での実行を想定。

1. アルゴリズム

当ブログ過去記事を参照。

• ロジスティック回帰分析！

2. Ruby スクリプトの作成

• 説明のために、随所にコメントを入れている。
• matrix クラスを拡張する形にしている。
• 今回は、説明変数2個を想定しているが、1個や3個以上でも計算可能。（のはず）
• Shebang ストリング（1行目）では、フルパスでコマンド指定している。（当方の慣習）

File: regression_logistic.rb

#! /usr/local/bin/ruby
#*********************************************
# Ruby script to compute a logistic regression analysis.
# (by extending the matrix class)
#*********************************************
#
require 'matrix'

class Matrix
  ALPHA = 0.01      # 学習率
  EPS   = 1.0e-12   # 閾値
  LOOP  = 10000000  # 最大ループ回数
  BETA  = 5.0       # 初期値: β
  CEL   = 0.0       # 初期値: 交差エントロピー誤差

  def reg_logistic
    # 元の数, サンプル数
    e = self.column_size - 1
    n = self.row_size
    # 自身 Matrix が空の場合は例外スロー
    raise "Self array is nil!" if self.empty?
    # β初期値 (1 行 e + 1 列)
    bs = Matrix.build(1, e + 1) { |_| BETA }
    # X の行列 (n 行 e 列)
    # (第1列(x_0)は定数項なので 1 固定)
    xs = Matrix.hstack(Matrix.build(n, 1) { 1 }, self.minor(0, n, 0, e))
    # t の行列 (n 行 1 列)
    ts = self.minor(0, n, e, 1)
    # 交差エントロピー誤差初期値
    loss = CEL
    LOOP.times do |i|
      #puts "i=#{i}"
      # シグモイド関数適用（予測値計算）
      ys = sigmoid(xs * bs.transpose)
      # dE 計算
      des = (ys - ts).transpose * xs / n
      # β 更新
      bs -= ALPHA * des
      # 前回算出交差エントロピー誤差退避
      loss_pre = loss
      # 交差エントロピー誤差計算
      loss = cross_entropy_loss(ts, ys)
      # 今回と前回の交差エントロピー誤差の差が閾値以下になったら終了
      break if (loss - loss_pre).abs < EPS
    end

    return bs
  end

private
  # シグモイド関数
  def sigmoid(x)
    return x.map { |a| 1.0 / (1.0 + Math.exp(-a)) }
  rescue => e
    raise
  end

  # 交差エントロピー誤差関数
  def cross_entropy_loss(ts, ys)
    return ts.zip(ys).map { |t, y|
      t * Math.log(y) + (1.0 - t) * Math.log(1.0 - y)
    }.sum
  rescue => e
    raise
  end
end

# 説明(独立)変数と目的(従属)変数
# （ e.g.  n 行 3 列 (x1, x2, y) )
data = Matrix[
  [30, 21, 0],
  [22, 10, 0],
  [26, 25, 0],
  [14, 20, 0],
  [ 6, 10, 1],
  [ 2, 15, 1],
  [ 6,  5, 1],
  [10,  5, 1],
  [19, 15, 1]
]
puts "data ="
data.to_a.each { |row| p row }

# ロジスティック回帰式の定数・係数計算(b0, b1, b2, ...)
puts "\nNow computing...\n\n"
reg_logistic = data.reg_logistic
puts "betas = "
p reg_logistic.to_a

• Gist - Ruby script to calculate a logistic regression.

3. Ruby スクリプトの実行

まず、実行権限を与える。

$ chmod +x logistic_regression.rb

そして、実行。

$ ./regression_logistic.rb
data =
[30, 21, 0]
[22, 10, 0]
[26, 25, 0]
[14, 20, 0]
[6, 10, 1]
[2, 15, 1]
[6, 5, 1]
[10, 5, 1]
[19, 15, 1]

Now computing...

betas =
[[8.993763519187013, -0.30784038300690836, -0.26681572350248417]]

ループ処理をしているので、処理にやや時間がかかるかもしれない。

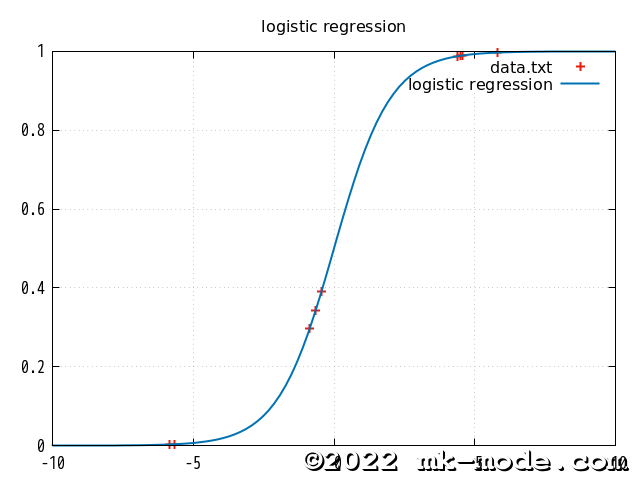
4. グラフ描画

gnuplot でグラフ描画してみた。

• 横軸は \(\beta_0+\beta_1x_1+\beta_2x_2\)
• 縦軸はシグモイド関数で算出した値 \(\frac{1}{1 + e^{-(\beta_0+\beta_1x_1+\beta_2x_2)}}\)）

---

C++ でも実装してみたいですが、行列計算に線形代数ライブラリ Eigen を使用してみたいので、そのライブラリの使用方法をある程度理解してから。

以上。