Ruby - Array クラス拡張で単回帰曲線計算!
Updated:
以前、 Ruby の Array クラスを拡張して単回帰直線を計算してみました。
今回は、同様に Ruby の Array クラスを拡張して回帰式が2次の単回帰曲線を計算してみました。(「直線」でなく「曲線」
0. 前提条件
- Ruby 2.5.0-p0 での作業を想定。
1. 単回帰曲線について
単回帰直線の一般形の部分を2次曲線 \(y = a + bx + cx^{2}\) として考えるだけ。
連立方程式を解くと、\(a,b,c\) は最終的に以下のようになる。
\[\begin{align} B &= \frac{S_{xy}S_{x^2x^2} - S_{x^2y}S_{xx^2}}{S_{xx}S_{x^2x^2} - (S_{xx^2})^2} \\ C &= \frac{S_{x^2y}S_{xx} - S_{xy}S_{xx^2}}{S_{xx}S_{x^2x^2} - (S_{xx^2})^2} \\ A &= \overline{y} - B\overline{x} - C\overline{x^2} \\ \end{align}\]但し、
\[\begin{align} S_{xx} &= \frac{\sum (x_{i} - \overline{x})^2}{n} = \frac{\sum x_{i}^{2}}{n} - \overline{x}^{2} \\ S_{xy} &= \frac{\sum (x_{i} - \overline{x})(y_{i} - \overline{y})}{n} = \frac{\sum x_{i}y_{i}}{n} - \overline{x} \ \overline{y} \\ S_{xx^{2}} &= \frac{\sum (x_{i} - \overline{x})(x_{i}^{2} - \overline{x^{2}})}{n} = \frac{\sum x_{i}^{3}}{n} - \overline{x}\overline{x^{2}} \\ S_{x^{2}x^{2}} &= \frac{\sum (x_{i}^{2} - \overline{x^{2}})^{2}}{n} = \frac{\sum x_{i}^{4}}{n} - \overline{x^{2}} \ \overline{x^{2}} \\ S_{x^{2}y} &= \frac{\sum (x_{i}^{2} - \overline{x^{2}})(y_{i} - \overline{y})}{n} = \frac{\sum x_{i}^{2}y_{i}}{n} - \overline{x^{2}}\overline{y} \end{align}\]ちなみに、回帰分析(回帰式)には、今回の曲線回帰(2次)の他に以下のようなものがある。(説明略)
- 直線回帰
- ルート回帰
- 自然対数回帰
- 分数回帰
- べき乗回帰
- 指数回帰
- 修正指数回帰
- ロジスティック回帰
- ゴンベルツ回帰
- etc…
2. Ruby スクリプト作成
以下のように Array クラスを拡張してメソッドを定義してみた。
File: regression_curve.rb
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#! /usr/local/bin/ruby
#*********************************************
# Ruby script to calculate a simple regression curve.
#*********************************************
#
class Array
def reg_line(y)
# 以下の場合は例外スロー
# - 引数の配列が Array クラスでない
# - 自身配列が空
# - 配列サイズが異なれば例外
raise "Argument is not a Array class!" unless y.class == Array
raise "Self array is nil!" if self.size == 0
raise "Argument array size is invalid!" unless self.size == y.size
n = self.size # number of items
m_x = self.sum / n.to_f # avg(X)
m_y = y.sum / n.to_f # avg(Y)
m_x2 = self.map { |x| x ** 2 }.sum / n.to_f # avg(X^2)
m_x3 = self.map { |x| x ** 3 }.sum / n.to_f # avg(X^3)
m_x4 = self.map { |x| x ** 4 }.sum / n.to_f # avg(X^4)
m_xy = self.zip(y).map { |a, b| a * b }.sum / n.to_f # avg(X * Y)
m_x2y = self.zip(y).map { |a, b| a * a * b }.sum / n.to_f # avg(X^2 * Y)
s_xx = m_x2 - m_x * m_x # Sxx
s_xy = m_xy - m_x * m_y # Sxy
s_xx2 = m_x3 - m_x * m_x2 # Sxx2
s_x2x2 = m_x4 - m_x2 * m_x2 # Sx2x2
s_x2y = m_x2y - m_x2 * m_y # Sx2y
b = s_xy * s_x2x2 - s_x2y * s_xx2
b /= s_xx * s_x2x2 - s_xx2 * s_xx2
c = s_x2y * s_xx - s_xy * s_xx2
c /= s_xx * s_x2x2 - s_xx2 * s_xx2
a = m_y - b * m_x - c * m_x2
{a: a, b: b, c: c}
end
end
# 説明変数と目的変数
#ary_x = [107, 336, 233, 82, 61, 378, 129, 313, 142, 428]
#ary_y = [286, 851, 589, 389, 158, 1037, 463, 563, 372, 1020]
ary_x = [83, 71, 64, 69, 69, 64, 68, 59, 81, 91, 57, 65, 58, 62]
ary_y = [183, 168, 171, 178, 176, 172, 165, 158, 183, 182, 163, 175, 164, 175]
puts "説明変数 X = {#{ary_x.join(', ')}}"
puts "目的変数 Y = {#{ary_y.join(', ')}}"
puts "---"
# 単回帰曲線算出
reg_line = ary_x.reg_line(ary_y)
puts "a = #{reg_line[:a]}"
puts "b = #{reg_line[:b]}"
puts "c = #{reg_line[:c]}"
3. Ruby スクリプト実行
まず、実行権限を付与。
$ chmod +x regression_curve.rb
そして、実行。
$ ./regression_curve.rb
説明変数 X = {83, 71, 64, 69, 69, 64, 68, 59, 81, 91, 57, 65, 58, 62}
目的変数 Y = {183, 168, 171, 178, 176, 172, 165, 158, 183, 182, 163, 175, 164, 175}
---
a = 41.374539640720556
b = 3.0867232029882175
c = -0.016835648076371865
4. 視覚的な確認
参考までに、上記スクリプトで使用した2変量の各点と作成された単回帰直線を R でグラフに描画してみた。
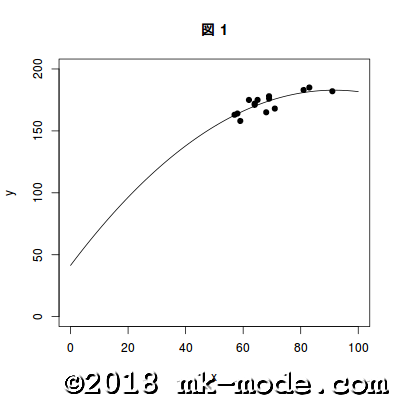
以上。

Comments