Fortran - 数値積分（台形則／シンプソン則による定積分）！

Fortran 95 で、数値積分（台形則／シンプソン則による定積分）行ってみました。

0. 前提条件

• LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
• GCC 6.3.0 (GFortran 6.3.0) でのコンパイルを想定。

1. 数値積分（台形則／シンプソン則による定積分）とは？

当ブログ過去記事を参照のこと。

• C++ - 数値積分（台形則による定積分）！
• C++ - 数値積分（シンプソン則による定積分）！

2. 想定する被積分関数

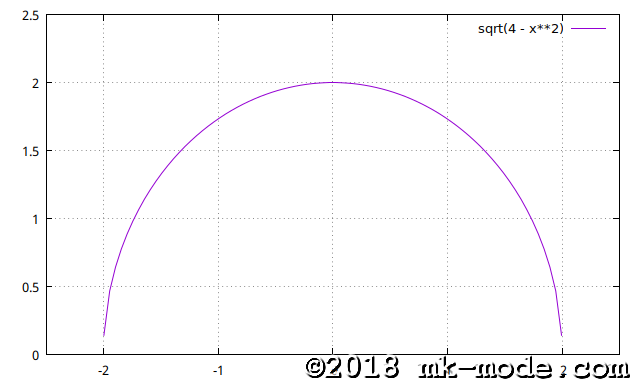
想定する被積分関数は \(f(x) = \sqrt{4 - x^{2}}\ \ (但し、 0.0 \leq x \leq 2.0\))

3. ソースコードの作成

• 台形則／シンプソン則計算部分はモジュール化している。
• 小さなファイルなので、モジュール部分を別ファイルには分けていない。

File: definite_integral.f95

!****************************************************
! 定積分（台形則、シンプソン則）
! * f = sqrt(4.0 - x**2)  (0.0 <= x <= 2.0)
!
! date          name            version
! 2018.10.13    mk-mode.com     1.00 新規作成
!
! Copyright(C) 2018 mk-mode.com All Rights Reserved.
!****************************************************
!
module integrator
  implicit none
  ! SP: 単精度(4), DP: 倍精度(8)
  integer,     parameter :: SP = kind(1.0)
  integer(SP), parameter :: DP = selected_real_kind(2 * precision(1.0_SP))
  real(DP),    parameter :: PI = atan(1.0_8) * 4.0_DP  ! 円周率

contains
  ! 数値積分（台形則）
  !
  ! :param  real(8) f(:)
  ! :param  real(8)   dx
  ! :return real(8)  ret
  function trapezoid(f, dx) result(ret)
    implicit none
    real(DP), intent(in) :: f(:)
    real(DP), intent(in) :: dx
    real(DP)    :: ret
    integer(SP) :: i, n

    n = size(f)
    ret = 0.5_DP * (f(1) + f(n))
    do i = 2, n - 1
       ret = ret + f(i)
    end do
    ret = ret * dx
  end function trapezoid

  ! 数値積分（シンプソン則）
  !
  ! :param  real(8)  f(:)
  ! :param  real(8)    dx
  ! :return real(8)   ret
  function simpson(f, dx) result(ret)
    implicit none
    real(DP), intent(in) :: f(:)
    real(DP), intent(in) :: dx
    real(DP)    :: ret
    integer(SP) :: i, n

    n = size(f)
    ! 端点を含めた配列サイズが奇数でなければ終了
    if (mod(n, 2) == 0) then
       write(*,*) '配列サイズが奇数でない！'
       stop
    end if
    ret = f(1) + f(n)
    ! （偶数）
    do i = 2, n - 1, 2
       ret = ret + 4.0_8 * f(i)
    end do
    ! （奇数）
    do i = 3, n - 2, 2
       ret = ret + 2.0_DP * f(i)
    end do
    ret = ret * dx / 3.0_DP
  end function simpson
end module integrator

program definite_integral
  use integrator
  implicit none
  integer(SP) :: n, nmax
  real(DP)    :: x_1, x_2, dx, integral
  real(DP), allocatable :: f_1(:), f_2(:)

  write(*, fmt='(A)', advance='no') '区間の数 : '
  read(*,*) nmax

  ! 配列用メモリ確保
  allocate(f_1(0:nmax))
  allocate(f_2(0:nmax))

  x_1 = 0.0_DP
  x_2 = 2.0_DP
  dx = (x_2 - x_1) / nmax

  ! 数値積分（台形則）
  do n = 0, nmax
    f_1(n) = f(x_1 + dx * real(n, 8))
  end do
  integral = trapezoid(f_1, dx)
  write (*, fmt='(a15, ": ", f18.15, " (誤差= ", e18.12, ")")') &
    & "台形則", integral, abs(integral / PI - 1.0_DP)

  ! 数値積分（シンプソン則）
  do n = 0, nmax
    f_2(n) = f(x_1 + dx * real(n, 8))
  end do
  integral = simpson(f_2, dx)
  write(*, fmt='(a18, ": ", f18.15, " (誤差= ", e18.12, ")")') &
       & "シンプソン則", integral, abs(integral / PI - 1.0_DP)

  ! 配列用メモリ解放
  deallocate(f_1)
  deallocate(f_2)

  stop
contains
  ! 被積分関数
  real(DP) function f(x)
    implicit none
    real(DP), intent(in) :: x

    f = sqrt(4.0_DP - x * x)
  end function f
end program definite_integral

• Gist - Fortran 95 source code to compute a definite integral.

4. ソースコードのコンパイル

$ gfortran -o definite_integral definite_integral.f95

5. 動作確認

区間を分割する数を問われるので、入力する。（シンプソン則にも対応するために偶数で指定する）

$ ./definite_integral
区間の数 : 100
      台形則:  3.140417031779045 (誤差= 0.374212044774E-03)
シンプソン則:  3.141133205339227 (誤差= 0.146246920345E-03)

---

以上、