Fortran - 重回帰式計算（説明変数2個）（その2）！

以前、 Fortran 95 で、説明（独立）変数2個、目的（従属）変数1個の「重回帰式」を計算する方法を紹介しました。但し、平方和／積和の行列を作成してからその行列（連立方程式）を解く方法でした。

• Fortran - 重回帰式計算（説明変数2個）！

今回は、直接、行列（偏微分後の連立方程式）を解く方法について紹介します。
（今回は、説明変数が2個のケースの他に、説明変数が3個のケースも）

0. 前提条件

• LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
• GCC 6.3.0 (GFortran 6.3.0) でのコンパイルを想定。

1. アルゴリズム

求める重回帰式を \(y=b_0+b_1x_1+b_2x_2\) （説明変数が2個の場合）とすると、残差の二乗和 \(S\) は

\[\begin{eqnarray*} S = \sum_{i=1}^{N}(y_i - b_0 - b_1x_{1i} - b_2x_{2i})^2 \end{eqnarray*}\]

となる。 \(b_0,b_1,b_2\) それぞれで偏微分したものを \(0\) とする。

\[\begin{eqnarray*} \frac{\partial S}{\partial b_0} &=& 2\sum_{i=1}^{N}(b_{0}+b_{1}x_{1i}+b_{2}x_{2i} - y_i) = 0 \\ \frac{\partial S}{\partial b_1} &=& 2\sum_{i=1}^{N}(b_{0}x_{1i}+b_{1}x_{1i}x_{1i}+b_2x_{1i}x_{2i} - x_{1i}y_i) = 0 \\ \frac{\partial S}{\partial b_2} &=& 2\sum_{i=1}^{N}(b_{0}x_{2i}+b_{1}x_{2i}x_{1i}+b_2x_{2i}x_{2i} - x_{2i}y_i) = 0 \end{eqnarray*}\]

これらを変形すると、

\[\begin{eqnarray*} b_{0}N + b_{1}\sum_{i=1}^{N}x_{1i} + b_{2}\sum_{i=1}^{N}x_{2i} &=& \sum_{i=1}^{N}y_i \\ b_{0}\sum_{i=1}^{N}x_{1i} + b_{1}\sum_{i=1}^{N}x_{1i}x_{1i} + b_{2}\sum_{i=1}^{N}x_{1i}x_{2i} &=& \sum_{i=1}^{N}x_{1i}y_i \\ b_{0}\sum_{i=1}^{N}x_{2i} + b_{1}\sum_{i=1}^{N}x_{2i}x_{1i} + b_{2}\sum_{i=1}^{N}x_{2i}x_{2i} &=& \sum_{i=1}^{N}x_{2i}y_i \end{eqnarray*}\]

となる。これらの連立1次方程式を解けばよい。

• 説明変数が3個の場合も同様。（項数や連立1次方程式の式が1個増えるだけ）

2. ガウスの消去法による連立方程式の解法について

当ブログ過去記事を参照。

• Ruby - 連立方程式解法（ガウスの消去法）！

3. ソースコードの作成

File: regression_multi_v2.f95

!****************************************************
! 重回帰式計算（説明（独立）変数2個限定）
! * 一旦、平方和／積和の行列を作成してから連立方程式
!   を解くのではなく、直接、偏微分後の連立方程式を解く。
!
!   date          name            version
!   2019.06.01    mk-mode.com     1.00 新規作成
!
! Copyright(C) 2018 mk-mode.com All Rights Reserved.
!****************************************************
!
module const
  ! SP: 単精度(4), DP: 倍精度(8)
  integer,     parameter :: SP = kind(1.0)
  integer(SP), parameter :: DP = selected_real_kind(2 * precision(1.0_SP))
end module const

module comp
  use const
  implicit none
  private
  public :: calc_reg_multi

contains
  ! 重回帰式計算
  ! * 説明変数2個限定
  !
  ! :param(in)  real(8) x(:, 2): 説明変数配列
  ! :param(in)  real(8)    y(:): 目的変数配列
  ! :param(out) real(8)       c: 定数
  ! :param(out) real(8)    v(2): 係数
  subroutine calc_reg_multi(x, y, c, v)
    implicit none
    real(DP), intent(in)  :: x(:, :), y(:)
    real(DP), intent(out) :: c, v(2)
    integer(SP) :: s_x1, s_x2, s_y, i
    real(DP)    :: sum_x1, sum_x1x1, sum_x1x2
    real(DP)    :: sum_x2, sum_x2x1, sum_x2x2
    real(DP)    :: sum_y, sum_x1y, sum_x2y
    real(DP)    :: mtx(3, 4)

    s_x1 = size(x(:, 1))
    s_x2 = size(x(:, 2))
    s_y  = size(y)
    if (s_x1 == 0 .or. s_x2 == 0 .or. s_y == 0) then
      print *, "[ERROR] array size == 0"
      stop
    end if
    if (s_x1 /= s_y .or. s_x2 /= s_y) then
      print *, "[ERROR] size(X) != size(Y)"
      stop
    end if

    sum_x1   = sum(x(:, 1))
    sum_x2   = sum(x(:, 2))
    sum_x1x1 = sum(x(:, 1) * x(:, 1))
    sum_x1x2 = sum(x(:, 1) * x(:, 2))
    sum_x2x1 = sum_x1x2
    sum_x2x2 = sum(x(:, 2) * x(:, 2))
    sum_y    = sum(y)
    sum_x1y  = sum(x(:, 1) * y)
    sum_x2y  = sum(x(:, 2) * y)
    mtx(1, :) = (/real(s_x1, DP),   sum_x1,   sum_x2,   sum_y/)
    mtx(2, :) = (/        sum_x1, sum_x1x1, sum_x1x2, sum_x1y/)
    mtx(3, :) = (/        sum_x2, sum_x2x1, sum_x2x2, sum_x2y/)
    call gauss_e(3, mtx)
    c = mtx(1, 4)
    v = mtx(2:3, 4)
  end subroutine calc_reg_multi

  ! Gaussian elimination
  !
  ! :param(in)    integer(4)     n: 元数
  ! :param(inout) real(8) a(n,n+1): 係数配列
  subroutine gauss_e(n, a)
    implicit none
    integer(SP), intent(in)    :: n
    real(DP),    intent(inout) :: a(n, n + 1)
    integer(SP) :: i, j
    real(DP)    :: d

    ! 前進消去
    do j = 1, n - 1
      do i = j + 1, n
        d = a(i, j) / a(j, j)
        a(i, j+1:n+1) = a(i, j+1:n+1) - a(j, j+1:n+1) * d
      end do
    end do

    ! 後退代入
    do i = n, 1, -1
      d = a(i, n + 1)
      do j = i + 1, n
        d = d - a(i, j) * a(j, n + 1)
      end do
      a(i, n + 1) = d / a(i, i)
    end do
  end subroutine gauss_e
end module comp

program regression_multi
  use const
  use comp
  implicit none
  character(9), parameter :: F_INP = "input.txt"
  integer(SP),  parameter :: UID   = 10
  real(DP)    :: c, v(2)
  integer(SP) :: n, i
  character(20) :: f
  real(DP), allocatable :: x(:, :), y(:)

  ! IN ファイル OPEN
  open (UID, file = F_INP, status = "old")

  ! データ数読み込み
  read (UID, *) n

  ! 配列用メモリ確保
  allocate(x(n, 2))
  allocate(y(n))

  ! データ読み込み
  do i = 1, n
    read (UID, *) x(i, :), y(i)
  end do
  write (f, '("(A, ", I0, "F8.2, A)")') n
  print f, "説明変数 X(1) = (", x(:, 1), ")"
  print f, "説明変数 X(2) = (", x(:, 2), ")"
  print f, "目的変数    Y = (", y, ")"
  print '(A)', "---"

  ! IN ファイル CLOSE
  close (UID)

  call calc_reg_multi(x, y, c, v)
  print '(A, F14.8)', "定数項 = ", c
  print '(A, F14.8)', "係数-1 = ", v(1)
  print '(A, F14.8)', "係数-2 = ", v(2)

  ! 配列用メモリ解放
  deallocate(x)
  deallocate(y)
end program regression_multi

• Gist - Fortran 95 source code to compute multiple regression equations.(v2)

4. ソースコードのコンパイル

$ gfortran -o regression_multi_v2 regression_multi_v2.f95

5. 動作確認

まず、以下のような入力ファイルを用意する。
（先頭行：点の数、2行目以降：各点）

File: input.txt

10
17.50 30.00 45.00
17.00 25.00 38.00
18.50 20.00 41.00
16.00 30.00 34.00
19.00 45.00 59.00
19.50 35.00 47.00
16.00 25.00 35.00
18.00 35.00 43.00
19.00 35.00 54.00
19.50 40.00 52.00

そして、実行。

$ ./regression_multi_v2
説明変数 X(1) = (   17.50   17.00   18.50   16.00   19.00   19.50   16.00  18.00   19.00   19.50)
説明変数 X(2) = (   30.00   25.00   20.00   30.00   45.00   35.00   25.00  35.00   35.00   40.00)
目的変数    Y = (   45.00   38.00   41.00   34.00   59.00   47.00   35.00  43.00   54.00   52.00)
---
定数項 =   -34.71293084
係数-1 =     3.46981263
係数-2 =     0.53300948

6. 視覚的な確認

参考までに、上記スクリプトで使用した2変量の各点と作成された単回帰曲線を gnuplot で描画してみた。

---

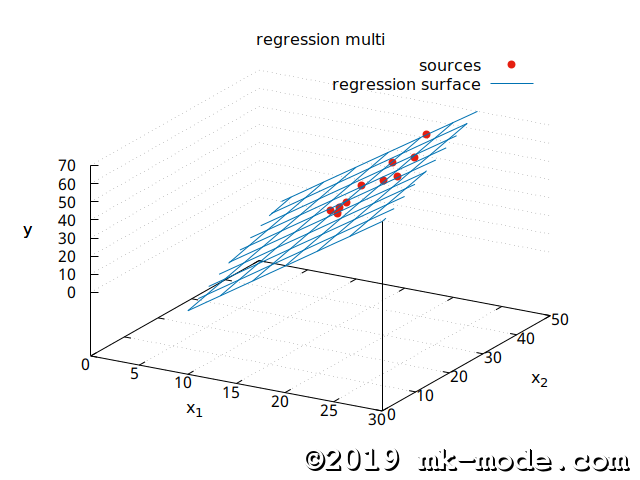
以上。