Ruby - Array クラスを拡張して重回帰分析（2次多項式モデル）！

過去に、説明（独立）変数2個、目的（従属）変数１個の「重回帰式」の計算を Ruby の Array クラスを拡張する方法で実装しました。

• Ruby - Array クラス拡張で重回帰式計算！

今回は、重回帰式を2次多項式にしてみました。

0. 前提条件

• LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
• Ruby 2.6.4 での作業を想定。

1. 重回帰式（2次多項式モデル）の求め方

求める重回帰式を \(y=b_0+b_1x_1+b_2x_2+b_3x_1x_2+b_4{x_1}^2+b_5{x_2}^2\) （説明変数が2個）とする場合、 \(x_3=x_1x_2,\ x_4={x_1}^2,\ x_5={x_2}^2\) と置くと、 \(y=b_0+b_1x_1+b_2x_2+b_3x_3+b_4x_4+b_5x_5\) （説明変数が5個）となるので、残差の二乗和 \(S\) は

\[\begin{eqnarray*} S = \sum(y_i - b_0 - b_1x_{1i} - b_2x_{2i} - b_3x_{3i} - b_4x_{4i} - b_5x_{5i})^2 \end{eqnarray*}\]

となる。 \(\displaystyle \left(\sum は \sum_{i=1}^{N}\right)\)

\(b_0,\cdots,b_5\) それぞれで偏微分したものを \(0\) とする。

\[\begin{eqnarray*} \frac{\partial S}{\partial b_0} &=& 2\sum(b_0+b_1x_{1i}+b_2x_{2i}+b_3x_{3i}+b_4x_{4i}+b_5x_{5i} - y_i) = 0 \\ \frac{\partial S}{\partial b_1} &=& 2\sum(b_0x_{1i}+b_1{x_{1i}}^2+b_2x_{1i}x_{2i}+b_3x_{1i}x_{3i}+b_4x_{1i}x_{4i}+b_5x_{1i}x_{5i} - x_{1i}y_i) = 0 \\ \frac{\partial S}{\partial b_2} &=& 2\sum(b_0x_{2i}+b_1x_{1i}x_{2i}+b_2{x_{2i}}^2+b_3x_{2i}x_{3i}+b_4x_{2i}x_{4i}+b_5x_{2i}x_{5i} - x_{2i}y_i) = 0 \\ \frac{\partial S}{\partial b_3} &=& 2\sum(b_0x_{3i}+b_1x_{1i}x_{3i}+b_2x_{2i}x_{3i}+b_3{x_{3i}}^2+b_4x_{3i}x_{4i}+b_5x_{3i}x_{5i} - x_{3i}y_i) = 0 \\ \frac{\partial S}{\partial b_4} &=& 2\sum(b_0x_{4i}+b_1x_{1i}x_{4i}+b_2x_{2i}x_{4i}+b_3x_{3i}x_{4i}+b_4{x_{4i}}^2+b_5x_{4i}x_{5i} - x_{4i}y_i) = 0 \\ \frac{\partial S}{\partial b_5} &=& 2\sum(b_0x_{5i}+b_1x_{1i}x_{5i}+b_2x_{2i}x_{5i}+b_3x_{3i}x_{5i}+b_4x_{4i}x_{5i}+b_5{x_{5i}}^2 - x_{5i}y_i) = 0 \end{eqnarray*}\]

これらを変形すると、

\[\begin{eqnarray*} b_0N + b_1\sum x_{1i} + b_2\sum x_{2i} + b_3\sum x_{3i} + b_4\sum x_{4i} + b_5\sum x_{5i} &=& \sum y_i \\ b_0\sum x_{1i}+b_1\sum {x_{1i}}^2+b_2\sum x_{1i}x_{2i}+b_3\sum x_{1i}x_{3i}+b_4\sum x_{1i}x_{4i}+b_5\sum x_{1i}x_{5i} &=& \sum x_{1i}y_i \\ b_0\sum x_{2i}+b_1\sum x_{1i}x_{2i}+b_2\sum {x_{2i}}^2+b_3\sum x_{2i}x_{3i}+b_4\sum x_{2i}x_{4i}+b_5\sum x_{2i}x_{5i} &=& \sum x_{2i}y_i \\ b_0\sum x_{3i}+b_1\sum x_{1i}x_{3i}+b_2\sum x_{2i}x_{3i}+b_3\sum {x_{3i}}^2+b_4\sum x_{3i}x_{4i}+b_5\sum x_{3i}x_{5i} &=& \sum x_{3i}y_i \\ b_0\sum x_{4i}+b_1\sum x_{1i}x_{4i}+b_2\sum x_{2i}x_{4i}+b_3\sum x_{3i}x_{4i}+b_4\sum {x_{4i}}^2+b_5\sum x_{4i}x_{5i} &=& \sum x_{4i}y_i \\ b_0\sum x_{5i}+b_1\sum x_{1i}x_{5i}+b_2\sum x_{2i}x_{5i}+b_3\sum x_{3i}x_{5i}+b_4\sum x_{4i}x_{5i}+b_5\sum {x_{5i}}^2 &=& \sum x_{5i}y_i \\ (但し、x_3=x_1x_2,\ x_4={x_1}^2,\ x_5={x_2}^2) \end{eqnarray*}\]

となる。これらの \(b_0,\cdots,b_5\) の連立1次方程式を解けばよい。
※\(x_3=x_1x_2,\ x_4={x_1}^2,\ x_5={x_2}^2\) と置かず、直接計算してもよいが、偏微分や連立方程式が煩雑になり、分かりにくくなる。

2. ガウスの消去法による連立方程式の解法について

当ブログ過去記事を参照。

• Ruby - 連立方程式解法（ガウスの消去法）！

3. Ruby スクリプトの作成

• Shebang ストリング（1行目）では、フルパスでコマンド指定している。（当方の慣習）

File: regression_multi_2d.rb

#! /usr/local/bin/ruby
#*********************************************
# Ruby script to calculate a multiple regression function(2D).
# * y = b0 + b1x1 + b2x2 + b3x1x2 + b4x1^2 + b5x2^2
#     これは、
#     y = b0 + b1x1 + b2x2 + b3x3 + b4x4 + b5x5
#     (但し、 x3 = x1x2, x4 = x1^2, x5 = x2^2)
#     と同じ。
#*********************************************
#
class Array
  def reg_multi_2d(y)
    # 元の数、変量内のサンプル数
    e_size, s_size = self.size, y.size
    # 以下の場合は例外スロー
    # - 引数の配列が Array クラスでない
    # - 自身配列が空
    # - 配列サイズが異なれば例外
    raise "Argument is not a Array class!"    unless y.class == Array
    raise "Self array is nil!"                if     e_size == 0
    raise "Argument array size is invalid!"   unless self[0].size == s_size
    1.upto(e_size - 1) do |i|
      raise "Argument array size is invalid!" unless self[0].size == self[i].size
    end
    x1, x2 = self
    x3 = x1.zip(x2).map { |a, b| a * b }
    x4 = x1.map { |a| a * a }
    x5 = x2.map { |a| a * a }
    mtx = Array.new(6).map { Array.new(7, 0.0) }
    # 左辺・対角成分
    mtx[0][0] = s_size
    mtx[1][1] = x1.map { |a| a * a }.sum
    mtx[2][2] = x2.map { |a| a * a }.sum
    mtx[3][3] = x3.map { |a| a * a }.sum
    mtx[4][4] = x4.map { |a| a * a }.sum
    mtx[5][5] = x5.map { |a| a * a }.sum
    # 左辺・右上成分
    mtx[0][1] = x1.sum
    mtx[0][2] = x2.sum
    mtx[0][3] = x3.sum
    mtx[0][4] = x4.sum
    mtx[0][5] = x5.sum
    mtx[1][2] = x1.zip(x2).map { |a, b| a * b }.sum
    mtx[1][3] = x1.zip(x3).map { |a, b| a * b }.sum
    mtx[1][4] = x1.zip(x4).map { |a, b| a * b }.sum
    mtx[1][5] = x1.zip(x5).map { |a, b| a * b }.sum
    mtx[2][3] = x2.zip(x3).map { |a, b| a * b }.sum
    mtx[2][4] = x2.zip(x4).map { |a, b| a * b }.sum
    mtx[2][5] = x2.zip(x5).map { |a, b| a * b }.sum
    mtx[3][4] = x3.zip(x4).map { |a, b| a * b }.sum
    mtx[3][5] = x3.zip(x5).map { |a, b| a * b }.sum
    mtx[4][5] = x4.zip(x5).map { |a, b| a * b }.sum
    # 左辺・左下成分
    mtx[1][0] = mtx[0][1]
    mtx[2][0] = mtx[0][2]
    mtx[2][1] = mtx[1][2]
    mtx[3][0] = mtx[0][3]
    mtx[3][1] = mtx[1][3]
    mtx[3][2] = mtx[2][3]
    mtx[4][0] = mtx[0][4]
    mtx[4][1] = mtx[1][4]
    mtx[4][2] = mtx[2][4]
    mtx[4][3] = mtx[3][4]
    mtx[5][0] = mtx[0][5]
    mtx[5][1] = mtx[1][5]
    mtx[5][2] = mtx[2][5]
    mtx[5][3] = mtx[3][5]
    mtx[5][4] = mtx[4][5]
    # 右辺
    mtx[0][6] = y.sum
    mtx[1][6] = x1.zip(y).map { |a, b| a * b }.sum
    mtx[2][6] = x2.zip(y).map { |a, b| a * b }.sum
    mtx[3][6] = x3.zip(y).map { |a, b| a * b }.sum
    mtx[4][6] = x4.zip(y).map { |a, b| a * b }.sum
    mtx[5][6] = x5.zip(y).map { |a, b| a * b }.sum
    # 連立方程式を解く (ガウスの消去法)
    return gauss_e(mtx)
  end

private
  # ガウスの消去法
  def gauss_e(ary)
    # 行数
    n = ary.size
    # 前進消去
    0.upto(n - 2) do |k|
      (k + 1).upto(n - 1) do |i|
        if ary[k][k] == 0
          puts "解けない！"
          exit 1
        end
        d = ary[i][k] / ary[k][k].to_f
        (k + 1).upto(n) do |j|
          ary[i][j] -= ary[k][j] * d
        end
      end
    end
    # 後退代入
    (n - 1).downto(0) do |i|
      if ary[i][i] == 0
        puts "解けない！"
        exit 1
      end
      d = ary[i][n]
      (i + 1).upto(n - 1) do |j|
        d -= ary[i][j] * ary[j][n]
      end
      ary[i][n] = d / ary[i][i].to_f
    end
    return ary.map { |a| a[-1] }
  end
end

# 説明(独立)変数と目的(従属)変数
ary_x = [
  [17.5, 17.0, 18.5, 16.0, 19.0, 19.5, 16.0, 18.0, 19.0, 19.5],
  [30, 25, 20, 30, 45, 35, 25, 35, 35, 40]
]
ary_y = [45, 38, 41, 34, 59, 47, 35, 43, 54, 52]
# 重回帰式算出(b0, b1, b2, ...)
reg_multi = ary_x.reg_multi_2d(ary_y)
# 結果出力
ary_x.each_with_index do |x, i|
  puts "説明変数 X#{i + 1} = {#{ary_x[i].join(', ')}}"
end
puts "目的変数 Y  = {#{ary_y.join(', ')}}"
puts "---"
p reg_multi

• Gist - Ruby script to calculate a multiple regression function.(2d)

4. Ruby スクリプトの実行

$ ./regression_multi_2d.rb
説明変数 X1 = {17.5, 17.0, 18.5, 16.0, 19.0, 19.5, 16.0, 18.0, 19.0, 19.5}
説明変数 X2 = {30, 25, 20, 30, 45, 35, 25, 35, 35, 40}
目的変数 Y  = {45, 38, 41, 34, 59, 47, 35, 43, 54, 52}
---
[-333.9032985981502, 45.8844170002146, -4.176065472613139, 0.21073632980137985, -1.384555099988024, 0.013710266583215294]

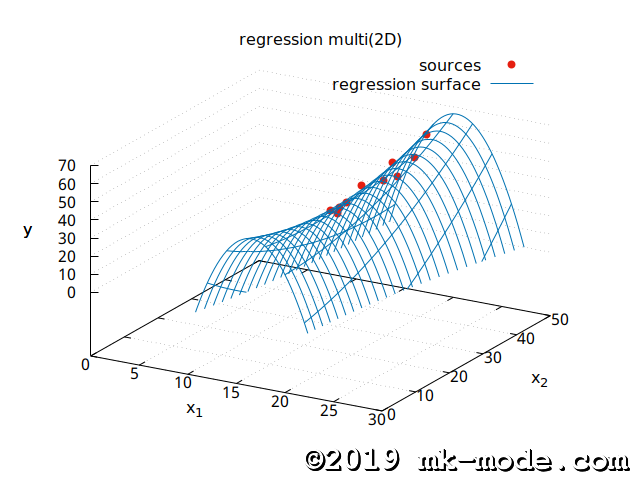
5. 視覚的な確認

参考までに、上記スクリプトで使用した2変量の各点と作成された単回帰曲線を gnuplot で描画してみた。

---

以上。