Ruby - Array クラス拡張で単回帰曲線（5次回帰モデル）計算！

かつて、 Ruby で Array クラスを拡張して単回帰直線や単回帰曲線（2〜4次、その他）を計算してみました。
（過去記事は「こちら」で検索してください）

今回は5次の単回帰曲線を計算してみました。自作のある解析処理で必要になったため、その練習として。（連立方程式の解法にはガウスの消去法（ピボット選択）を使用）

0. 前提条件

• Debian GNU/Linux 11.3 での作業を想定。
• Ruby 3.1.2 での実行を想定。
• 連立方程式の解法（ガウスの消去法（ピボット選択））についての説明は割愛。（Web 上等で容易に確認可能）

1. 単回帰曲線（5次回帰モデル）の求め方

求める曲線を \(y=a+bx+cx^2+dx^3+ex^4+fx^5\) とすると、残差の二乗和 \(S\) は

\[S = \sum_{i=1}^{N}(y_i - a - bx_i - cx_i^2 - dx^3 - ex^4 - fx^5)^2\]

となる。 \(a,b,c,d,e,f\) それぞれで偏微分したものを \(0\) とする。

\[\begin{eqnarray*} \frac{\partial S}{\partial a} &=& 2\sum_{i=1}^{N}(a+bx_i+cx_i^2+dx_i^3+ex_i^4+fx_i^5 - y_i) = 0 \\ \frac{\partial S}{\partial b} &=& 2\sum_{i=1}^{N}(ax_i+bx_i^2+cx_i^3+dx_i^4+ex_i^5+fx_i^6 - x_{i}y_i) = 0 \\ \frac{\partial S}{\partial c} &=& 2\sum_{i=1}^{N}(ax_i^2+bx_i^3+cx_i^4+dx_i^5+ex_i^6+fx_i^7 - x_{i}^{2}y_i) = 0 \\ \frac{\partial S}{\partial d} &=& 2\sum_{i=1}^{N}(ax_i^3+bx_i^4+cx_i^5+dx_i^6+ex_i^7+fx_i^8 - x_{i}^{3}y_i) = 0 \\ \frac{\partial S}{\partial e} &=& 2\sum_{i=1}^{N}(ax_i^4+bx_i^5+cx_i^6+dx_i^7+ex_i^8+fx_i^9 - x_{i}^{4}y_i) = 0 \\ \frac{\partial S}{\partial f} &=& 2\sum_{i=1}^{N}(ax_i^5+bx_i^6+cx_i^7+dx_i^8+ex_i^9+fx_i^{10} - x_{i}^{5}y_i) = 0 \end{eqnarray*}\]

これらを変形すると、

\[\begin{eqnarray*} aN + b\sum_{i=1}^{N}x_i + c\sum_{i=1}^{N}x_i^2 + d\sum_{i=1}^{N}x_i^3 + e\sum_{i=1}^{N}x_i^4 + f\sum_{i=1}^{N}x_i^5 &=& \sum_{i=1}^{N}y_i \\ a\sum_{i=1}^{N}x_i + b\sum_{i=1}^{N}x_i^2 + c\sum_{i=1}^{N}x_i^3 + d\sum_{i=1}^{N}x_i^4 + e\sum_{i=1}^{N}x_i^5 + f\sum_{i=1}^{N}x_i^6 &=& \sum_{i=1}^{N}x_{i}y_i \\ a\sum_{i=1}^{N}x_i^2 + b\sum_{i=1}^{N}x_i^3 + c\sum_{i=1}^{N}x_i^4 + d\sum_{i=1}^{N}x_i^5 + e\sum_{i=1}^{N}x_i^6 + f\sum_{i=1}^{N}x_i^7 &=& \sum_{i=1}^{N}x_{i}^{2}y_i \\ a\sum_{i=1}^{N}x_i^3 + b\sum_{i=1}^{N}x_i^4 + c\sum_{i=1}^{N}x_i^5 + d\sum_{i=1}^{N}x_i^6 + e\sum_{i=1}^{N}x_i^7 + f\sum_{i=1}^{N}x_i^8 &=& \sum_{i=1}^{N}x_{i}^{3}y_i \\ a\sum_{i=1}^{N}x_i^4 + b\sum_{i=1}^{N}x_i^5 + c\sum_{i=1}^{N}x_i^6 + d\sum_{i=1}^{N}x_i^7 + e\sum_{i=1}^{N}x_i^8 + f\sum_{i=1}^{N}x_i^9 &=& \sum_{i=1}^{N}x_{i}^{4}y_i \\ a\sum_{i=1}^{N}x_i^5 + b\sum_{i=1}^{N}x_i^6 + c\sum_{i=1}^{N}x_i^7 + d\sum_{i=1}^{N}x_i^8 + e\sum_{i=1}^{N}x_i^9 + f\sum_{i=1}^{N}x_i^{10} &=& \sum_{i=1}^{N}x_{i}^{5}y_i \end{eqnarray*}\]

となる。これらの連立方程式を解けばよい。

2. ガウスの消去法による連立方程式の解法について

当ブログ過去記事を参照。

• Ruby - 連立方程式解法（ガウスの消去法）！

3. Ruby スクリプトの作成

• Shebang ストリング（1行目）では、フルパスでコマンド指定している。（当方の慣習）

File: regression_curve_5d.rb

#! /usr/local/bin/ruby
#*********************************************
# Ruby script to calculate a simple regression curve.
# : y = a + b * x + c * x^2 + d * x^3 + e * x^4 + f * x^5
# : 連立方程式を ガウスの消去法（ピボット選択）で解く方法
#*********************************************
#
class Array
  def reg_curve_5d(y)
    # 以下の場合は例外スロー
    # - 引数の配列が Array クラスでない
    # - 自身配列が空
    # - 配列サイズが異なれば例外
    raise "Argument is not a Array class!"  unless y.class == Array
    raise "Self array is nil!"              if self.size == 0
    raise "Argument array size is invalid!" unless self.size == y.size

    sum_x   = self.inject(0) { |s, a| s += a }
    sum_x2  = self.inject(0) { |s, a| s += a * a }
    sum_x3  = self.inject(0) { |s, a| s += a * a * a }
    sum_x4  = self.inject(0) { |s, a| s += a * a * a * a }
    sum_x5  = self.inject(0) { |s, a| s += a * a * a * a * a }
    sum_x6  = self.inject(0) { |s, a| s += a * a * a * a * a * a }
    sum_x7  = self.inject(0) { |s, a| s += a * a * a * a * a * a * a }
    sum_x8  = self.inject(0) { |s, a| s += a * a * a * a * a * a * a * a }
    sum_x9  = self.inject(0) { |s, a| s += a * a * a * a * a * a * a * a * a }
    sum_x10 = self.inject(0) { |s, a| s += a * a * a * a * a * a * a * a * a * a }
    sum_y   = y.inject(0) { |s, a| s += a }
    sum_xy  = self.zip(y).inject(0) {
      |s, a| s += a[0] * a[1]
    }
    sum_x2y = self.zip(y).inject(0) {
      |s, a| s += a[0] * a[0] * a[1]
    }
    sum_x3y = self.zip(y).inject(0) {
      |s, a| s += a[0] * a[0] * a[0] * a[1]
    }
    sum_x4y = self.zip(y).inject(0) {
      |s, a| s += a[0] * a[0] * a[0] * a[0] * a[1]
    }
    sum_x5y = self.zip(y).inject(0) {
      |s, a| s += a[0] * a[0] * a[0] * a[0] * a[0] * a[1]
    }
    mtx = [
      [self.size,  sum_x, sum_x2, sum_x3, sum_x4, sum_x5,    sum_y],
      [    sum_x, sum_x2, sum_x3, sum_x4, sum_x5, sum_x6,   sum_xy],
      [   sum_x2, sum_x3, sum_x4, sum_x5, sum_x6, sum_x7,  sum_x2y],
      [   sum_x3, sum_x4, sum_x5, sum_x6, sum_x7, sum_x8,  sum_x3y],
      [   sum_x4, sum_x5, sum_x6, sum_x7, sum_x8, sum_x9,  sum_x4y],
      [   sum_x5, sum_x6, sum_x7, sum_x8, sum_x9, sum_x10, sum_x5y]
    ]
    ans = solve_ge(mtx)
    {
      a: ans[0][-1], b: ans[1][-1], c: ans[2][-1],
      d: ans[3][-1], e: ans[4][-1], f: ans[5][-1]
    }
  end

private

  # ピボット選択
  def pivot(a, k)
    pv = k
    v_max = a[k][k].abs
    (k + 1).upto(a.size - 1) do |i|
      if a[i][k].abs > v_max
        pv = i
        v_max = a[i][k].abs
      end
    end
    if k != pv
      dummy = a[k]
      a[k]  = a[pv]
      a[pv] = dummy
    end
    return a
  rescue => e
    raise
  end

  # 連立方程式の解（ガウスの消去法（ピボット選択））
  def solve_ge(a)
    n = a.size
    # 前進消去
    (n - 1).times do |k|
      a = pivot(a, k)  # ピボット選択処理
      (k + 1).upto(n - 1) do |i|
        d = a[i][k] / a[k][k].to_f
        (k + 1).upto(n) do |j|
          a[i][j] -= a[k][j] * d
        end
      end
    end
    # 後退代入
    (n - 1).downto(0) do |i|
      d = a[i][n]
      (i + 1).upto(n - 1) do |j|
        d -= a[i][j] * a[j][n]
      end
      a[i][n] = d / a[i][i].to_f
    end
    return a
  end
end

# 説明変数と目的変数
#ary_x = [107, 336, 233, 82, 61, 378, 129, 313, 142, 428]
#ary_y = [286, 851, 589, 389, 158, 1037, 463, 563, 372, 1020]
ary_x = [83, 71, 64, 69, 69, 64, 68, 59, 81, 91, 57, 65, 58, 62]
ary_y = [183, 168, 171, 178, 176, 172, 165, 158, 183, 182, 163, 175, 164, 175]
puts "説明変数 X = {#{ary_x.join(', ')}}"
puts "目的変数 Y = {#{ary_y.join(', ')}}"
puts "---"

# 単回帰曲線算出
reg_line = ary_x.reg_curve_5d(ary_y)
puts "a = #{reg_line[:a]}"
puts "b = #{reg_line[:b]}"
puts "c = #{reg_line[:c]}"
puts "d = #{reg_line[:d]}"
puts "e = #{reg_line[:e]}"
puts "f = #{reg_line[:f]}"

• Gist - Ruby script to calculate a simple regression curve.(5d)

4. Ruby スクリプトの実行

$ ./regression_curve_5d.rb
説明変数 X = {83, 71, 64, 69, 69, 64, 68, 59, 81, 91, 57, 65, 58, 62}
目的変数 Y = {183, 168, 171, 178, 176, 172, 165, 158, 183, 182, 163, 175, 164, 175}
---
a = 49990.925987311384
b = -3652.1635654342167
c = 106.05761790656705
d = -1.5255030925653301
e = 0.010870351512115147
f = -3.0701036411184224e-05

5. 視覚的な確認

参考までに、上記スクリプトで使用した2変量の各点と作成された単回帰曲線を gnuplot で描画してみた。（比較用に2次、3次、4次も）

---

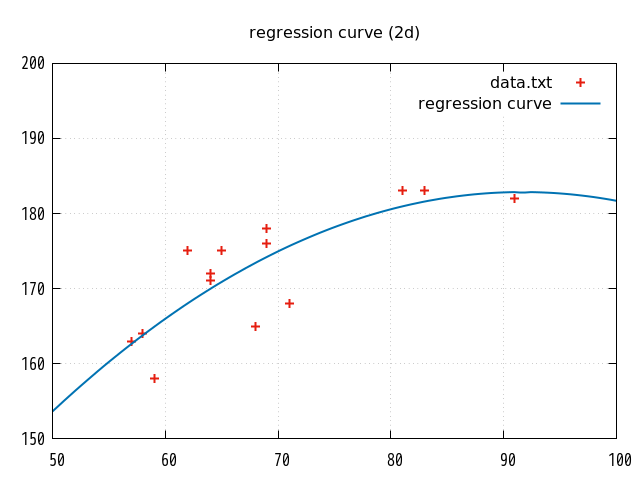
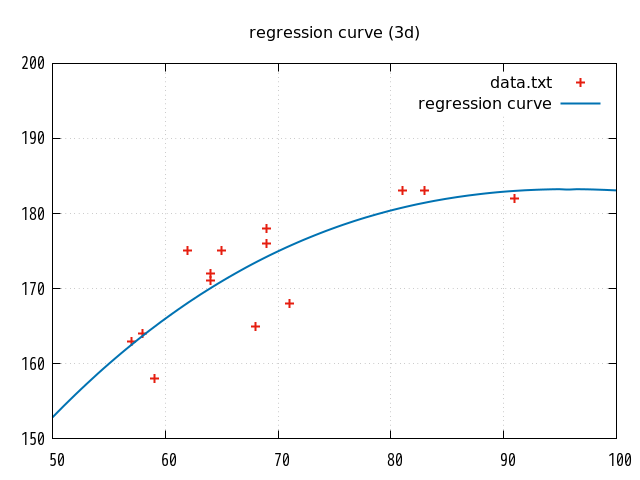
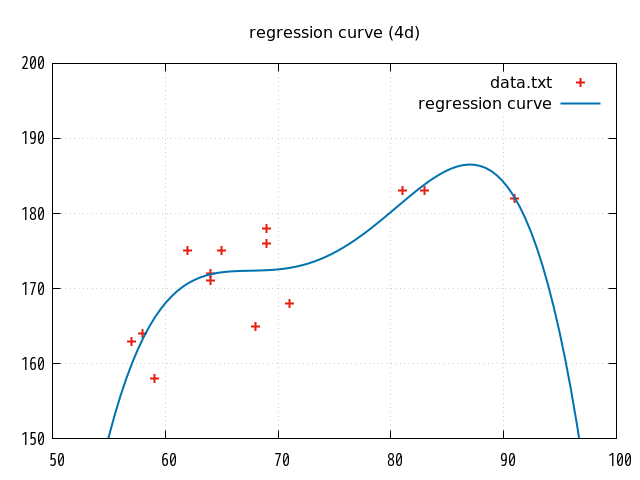
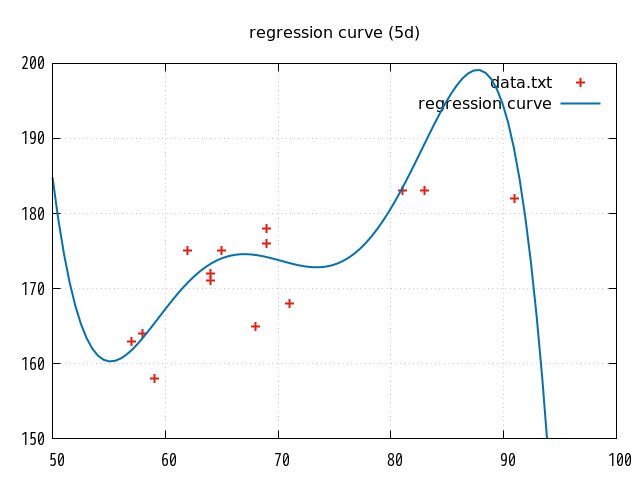
単回帰曲線の6次以降はもう試さない（つもり）。

以上。