Ruby - Array クラス拡張で単回帰直線計算(Ver.2)!
Updated:
Ruby で Array クラスを拡張して単回帰直線の切片と傾きを計算してみました。
※今回は連立1次方程式を解くのに「ガウスの消去法」を使用。
過去にも行いましたが、その際は連立1次方程式を解くのに分散/共分散を使用する方法(実際にはその変形版)を使用しました。
0. 前提条件
- LMDE 3 (Linux Mint Debian Edition 3; 64bit) での作業を想定。
- Ruby 2.6.3 での作業を想定。
1. ガウスの消去法による連立1次方程式の解法について
当ブログ過去記事を参照。
2. Ruby スクリプトの作成
- Shebang ストリング(1行目)では、フルパスでコマンド指定している。(当方の慣習)
File: regression_line_2.rb
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#! /usr/local/bin/ruby
#*********************************************
# Ruby script to calculate a simple lenear regression line.
# : y = a + b * x
# : 連立方程式を ガウスの消去法で解く方法
#*********************************************
#
class Array
def reg_line(y)
# 以下の場合は例外スロー
# - 引数の配列が Array クラスでない
# - 自身配列が空
# - 配列サイズが異なれば例外
raise "Argument is not a Array class!" unless y.class == Array
raise "Self array is nil!" if self.size == 0
raise "Argument array size is invalid!" unless self.size == y.size
sum_x = self.inject(0) { |s, a| s += a }
sum_y = y.inject(0) { |s, a| s += a }
sum_xx = self.inject(0) { |s, a| s += a * a }
sum_xy = self.zip(y).inject(0) { |s, a| s += a[0] * a[1] }
mtx = [
[self.size, sum_x, sum_y],
[ sum_x, sum_xx, sum_xy]
]
ans = solve_ge(mtx)
{intercept: ans[0][-1], slope: ans[1][-1]}
end
private
# 連立方程式の解(ガウスの消去法)
def solve_ge(a)
n = a.size
# 前進消去
(n - 1).times do |k|
(k + 1).upto(n - 1) do |i|
d = a[i][k] / a[k][k].to_f
(k + 1).upto(n) do |j|
a[i][j] -= a[k][j] * d
end
end
end
# 後退代入
(n - 1).downto(0) do |i|
d = a[i][n]
(i + 1).upto(n - 1) do |j|
d -= a[i][j] * a[j][n]
end
a[i][n] = d / a[i][i].to_f
end
return a
end
end
# 説明変数と目的変数
ary_x = [107, 336, 233, 82, 61, 378, 129, 313, 142, 428]
ary_y = [286, 851, 589, 389, 158, 1037, 463, 563, 372, 1020]
puts "説明変数 X = {#{ary_x.join(', ')}}"
puts "目的変数 Y = {#{ary_y.join(', ')}}"
puts "---"
# 単回帰直線算出(切片と傾き)
reg_line = ary_x.reg_line(ary_y)
puts "切片 a = #{reg_line[:intercept]}"
puts "傾き b = #{reg_line[:slope]}"
3. Ruby スクリプトの実行
$ ./regression_line_2.rb
説明変数 X = {107, 336, 233, 82, 61, 378, 129, 313, 142, 428}
目的変数 Y = {286, 851, 589, 389, 158, 1037, 463, 563, 372, 1020}
---
切片 a = 99.07475877245778
傾き b = 2.1445235003510286
4. 視覚的な確認
参考までに、上記スクリプトで使用した2変量の各点と作成された単回帰直線を gnuplot で描画してみた。
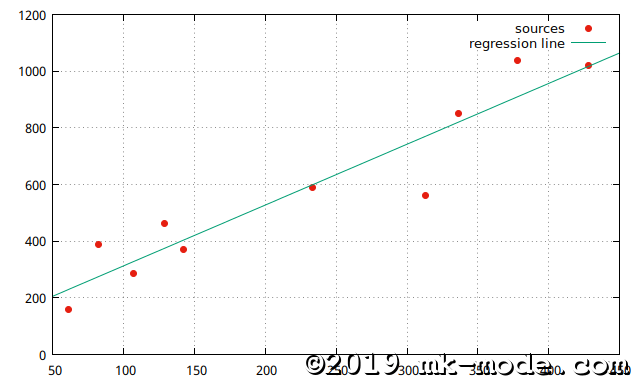
以上。

Comments